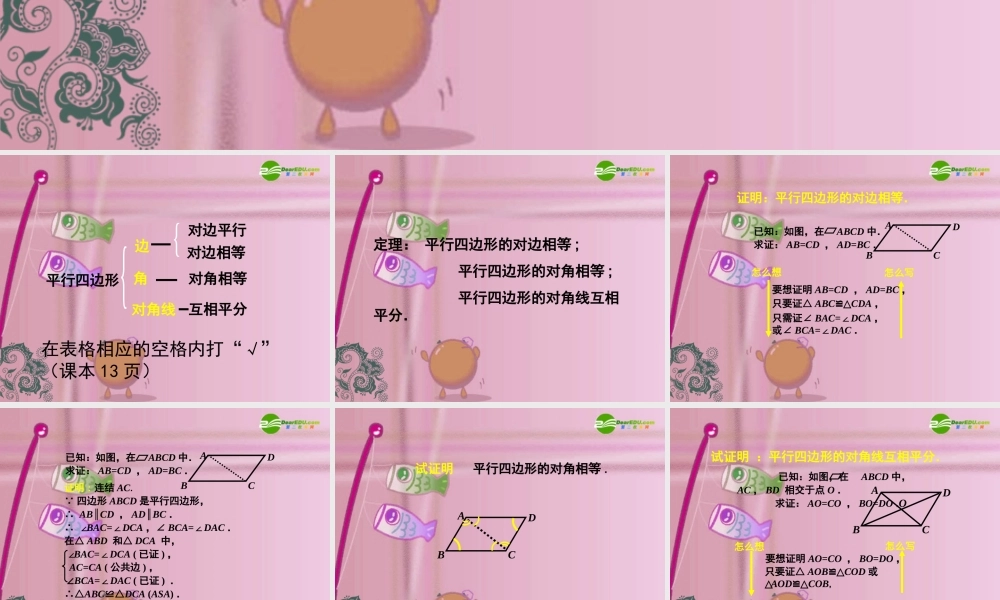
§3.3.1 平行四边形的性质 平行四边形对边平行边{角对角线{ 对边相等对角相等互相平分在表格相应的空格内打“√”(课本 13 页)定理: 平行四边形的对边相等 ; 平行四边形的对角相等 ; 平行四边形的对角线互相平分.要想证明 AB=CD , AD=BC ,只需证∠ BAC=∠DCA ,或∠ BCA=∠DAC .怎么想怎么写只要证△ ABC≌△CDA ,ADBC已知:如图,在 ABCD 中.求证: AB=CD , AD=BC . 证明:平行四边形的对边相等.证明 : 连结 AC. 四边形 ABCD 是平行四边形,∴ AB∥CD , AD∥BC .∴ ∠BAC=∠DCA ,∠ BCA=∠DAC .在△ ABD 和△ DCA 中, ∠BAC=∠DCA ( 已证 ) , AC=CA ( 公共边 ) , ∠BCA=∠DAC ( 已证 ) .∴△ABC≌△DCA (ASA) .∴AB=CD , AD=BC( 全等三角形的对应边相等 ) .ADBC已知:如图,在 ABCD 中.求证: AB=CD , AD=BC . 试证明 平行四边形的对角相等 .ADBC试证明 :平行四边形的对角线互相平分.要想证明 AO=CO , BO=DO ,怎么想怎么写只要证△ AOB≌△COD 或△AOD≌△COB, 已知:如图,在 ABCD 中, AC , BD 相交于点 O . 求证: AO=CO , BO=DO . ADBCO证明: 四边形 ABCD 是平行四边形,∴AB∥CD , AD∥BC ( 平行四边形的定义 ) , AB=CD ( 平行四边形的对边相等 ) .∴∠1=∠2 ,∠ 3=∠4 .在△ AOB 和△ COD 中, ∠1=∠2( 已证 ) , AB=CD( 已证 ) ,∠3=∠4( 已证 ) ,∴△AOB≌△COD(ASA) .∴AO=CO , BO=DO( 全等三角形的对应边相等 ) . 已知:如图,在 ABCD 中, AC,BD 相交于点 O . 求证: AO=CO , BO=DO . ADBCO1234定理 平行四边形的对角线互相 平分. 定理 平行四边形的对角相等.定理 平行四边形的对边相等.ADBC已知:如图,在 ABCD 中.求证:∠ A=∠C ,∠ B=∠D . 证明 : 四边形 ABCD 是平行四边形,∴ AB∥CD , AD∥BC .∴ ∠B+∠C=180° , ∠ A+∠B=180° .∴ ∠A=∠C .同理可得,∠ B=∠D . 已知:如图,在 ABCD 中, AC , BD 相交于点 O . 求证: AO=CO , BO=DO . 要想证明 AO=CO , BO=DO ,只需证 AB=CD ,怎么想怎么写只要证△ AOB≌△COD ,ADBCO只需证△ ABC≌△CDA .证明: 四边形 ABCD 是平行四边形,∴AB∥CD , AD∥BC .∴∠1=∠2 ,...