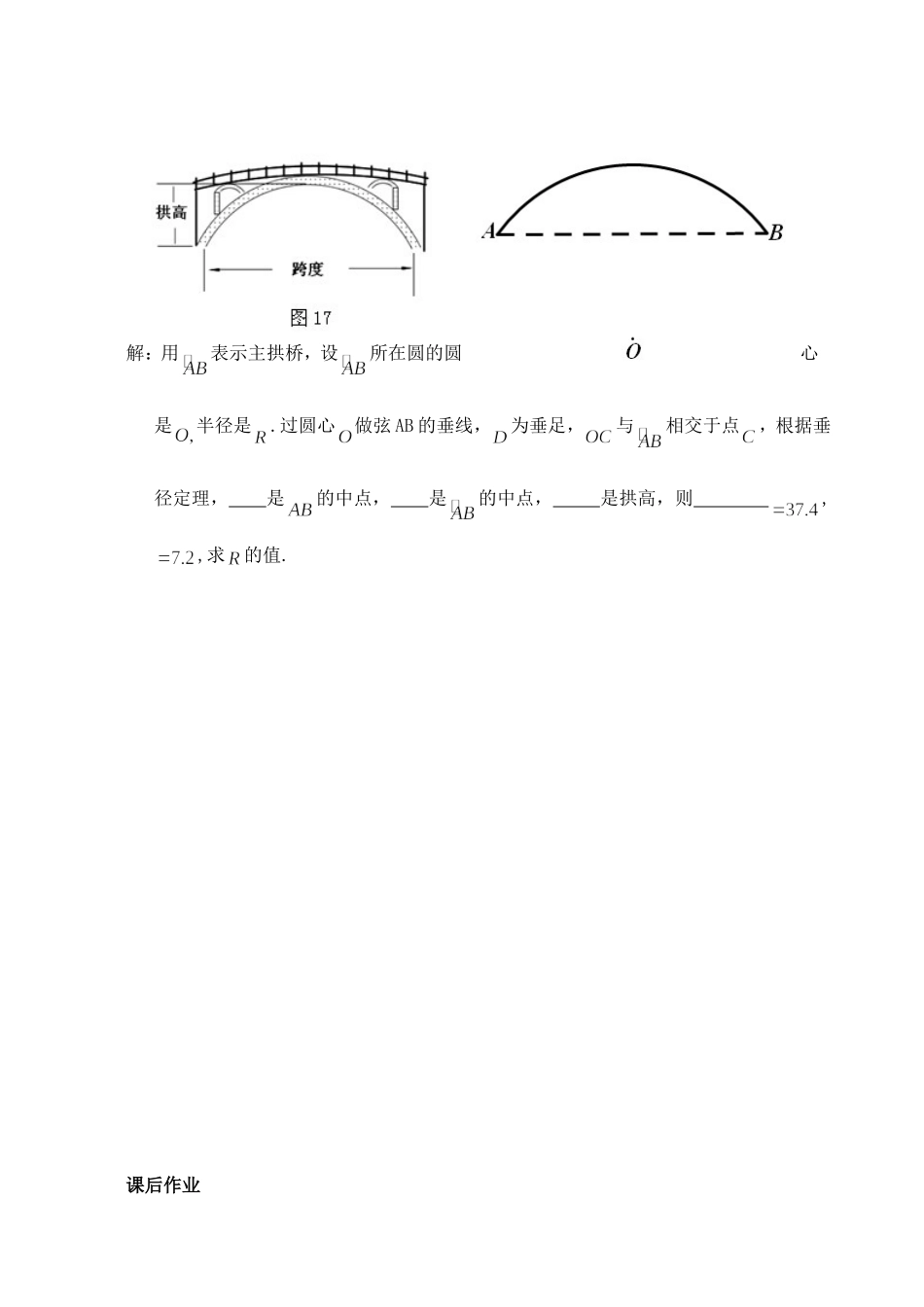
2 垂直于弦的直径（学卷）班级 姓名 1、我们已经学习了圆怎样的对称性质
2、圆还有什么对称性质
作为轴对称图形，其对称轴在哪里
请在自己作的圆中作图：(1)任意作一条弦；(2)过圆心作的垂线得直径且交于（如图 4）大胆猜想【问题 1】非直径弦在怎样情况下会被直径平分
猜想 1： 【问题 2】当弦被直径平分时，直径两侧相邻的两条弧是否也相等
即 弦所 对 的 两 条 弧和是否被平分
猜想 2： 证明你的猜想 1根据你的猜想，写出已知、求证
如图 5，已知： 求证：
证明：证明了你的猜想，它就是一个定理啦
请把你证明的定理用几何语言表达：即时巩固（应用你的定理）1
如图 14，在中，弦 8，圆心到的距离3，则的半径 2
如图 15，的半径，弦，则圆心到弦的距离
定 理 的 推论平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧
如图，已知是的直径，是的弦且
证明：【例 1】赵州桥是我国古代劳动人民勤劳与智慧的结晶，它的主拱桥是圆弧形，跨度是米，拱高是米
求出赵州桥主拱桥的半径（结果保留小数点后一位）
解：用表示主拱桥，设所在圆的圆心是半径是
过圆心做弦 AB 的垂线，为垂足，与相交于点，根据垂径定理， 是的中点， 是的中点， 是拱高，则 , ,求的值
（课本 90 页第 9 题）已知：如图，两个圆都以点为圆心，交大圆的弦交、小圆于两点
再添加一个同心圆，得（图 2）则 (填或 =)
隐去（图 1）中的大圆，得（图 3）连接，设，求证：
隐去（图 1）中的大圆，得（图 4）连接，设求证：
如图 16，的直径，弦， 是弦上的一个动点，那么的取值范围是
如图 19，圆弧形桥拱的跨度＝12 米，拱高＝4 米，则拱桥的半径为（ ） A．6
5 米 B．9 米 C．13 米 D．15 米 4
