平面和平面垂直的判定VIP免费

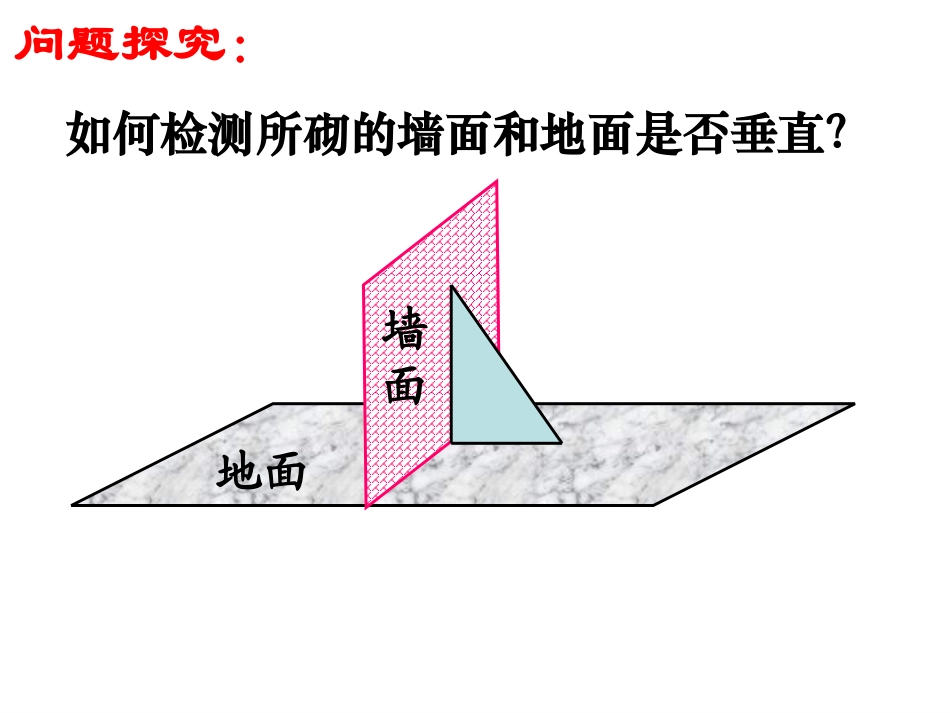
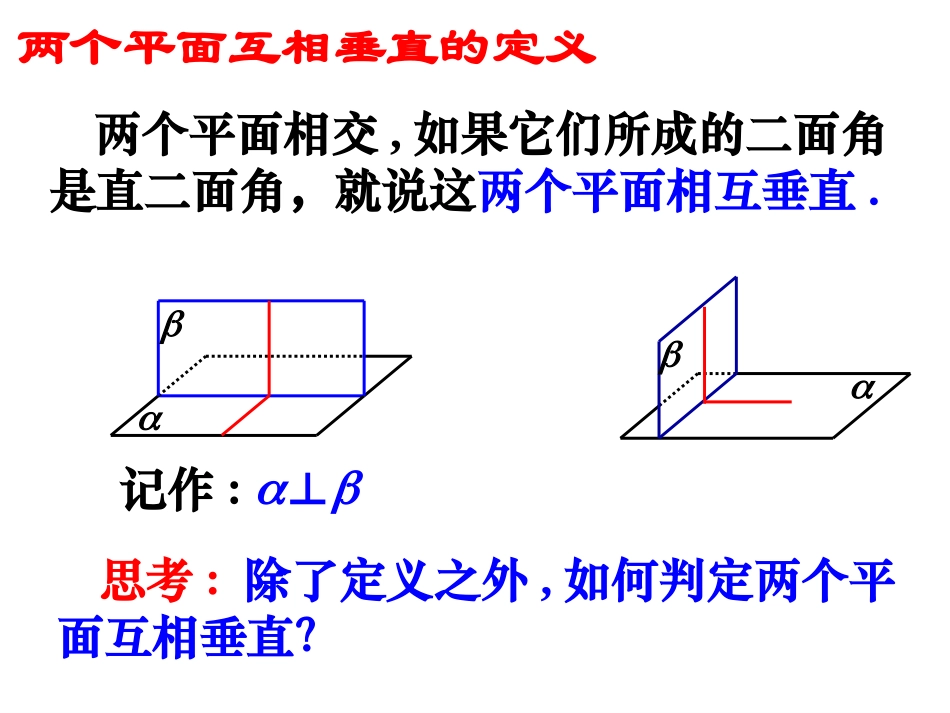
平面与平面垂直的判定如何检测所砌的墙面和地面是否垂直？问题探究：地面墙面两个平面互相垂直的定义两个平面相交,如果它们所成的二面角是直二面角，就说这两个平面相互垂直.记作:⊥思考:除了定义之外,如何判定两个平面互相垂直？.:,,,:,求证且已知如图BABABABC在平面内过B点作直线BC⊥l，则∠ABC就是二面角－l－的平面角，所以二面角－l－是直二面角，证明:,,lBl则设,,lAB.lAB,,BCAB.BCAB.ABl一个平面过另一个平面的垂线,则这两个平面垂直.面面垂直的判定定理:找垂直于平面的直线符号语言:作用:用法:ll线面垂直面面垂直Ol2.若平面内有一条直线垂直于平面内无数条直线，则一定有⊥.()4.若平面与不垂直,则平面内所有直线与都不垂直.()1.二面角的大小与其平面角的顶点在棱上的位置没有关系.()√√√3.若平面内有一条直线垂直于平面内两条相交直线，则一定有⊥.()判断题×5.过平面的一条垂线可作_____个平面与平面垂直.6.过一点可作____个平面与已知平面垂直.7.过平面的一条斜线，可作____个平面与平面垂直.8.过平面的一条平行线可作____个平面与平面垂直.1无数无数1填空题;)1(ABDAEC平面求证：平面.)2(CBDAEC平面求证：平面.90°,,.1的中点是，,所在平面外一点是如图例BDEADCABCADABBCDA△ABDCE例2.四边形ABCD是正方形,O是正方形的中心,且PO⊥平面ABCD,E是PC的中点.求证：平面PAC⊥平面BDE.APBCDOE例3.如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A、B的任意一点.ABPO.C(1)三棱锥的四个面的形状如何？都是直角三角形(2)图中有哪些面互相垂直？平面PAC⊥平面ABC平面PAB⊥平面ABC平面PAC⊥平面PBC(3)你能找到二面角P－BC－A的一个平面角吗？∠PCA1.如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,G1,G2,G3三点重合,重合后记为G－SEF,则四面体S－EFG中必有().A.SG⊥△EFG所在平面;B.SD⊥△EFG所在平面;C.GF⊥△SEF所在平面;D.GD⊥△SEF所在平面.练习SG1G2G3EFSEFGSGEFA1.如图,△ABC是等腰直角三角形,∠BAC＝90°,AB＝AC＝1,将△ABC沿斜边BC上的高AD折叠,使平面ABD⊥平面ACD,则折叠后BC＝.金榜P45类型二【典型例题】ABCDABCD【互动探究】若题1中将△ABC沿与AC平行的中位线DE折叠,使平面BDE⊥平面ACDE,试求BC.ABCDEDACBE所以∠AEB是二面角A-DE-B的平面角.因为平面BDE⊥平面ACDE,所以BE⊥平面ACDE,所以BE⊥EC.在△BCE中∠BEC=90°,1BE,2222215156CE()1,BC()().22222所以【解析】因为BE⊥DE,AE⊥DE,2.如图,正方体ABCD－A1B1C1D1中,E是AA1的中点.求证:平面C1BD⊥平面BDE.ABCDA1B1C1D1OE设AC∩BD=O,则O为BD的中点,连接C1O,EO,C1E.因为EB=ED,点O是BD的中点,所以BD⊥EO.因为C1B=C1D,点O是BD的中点,所以BD⊥C1O,所以∠C1OE即为二面角C1-BD-E的平面角.【解析】因为E为AA1中点,设正方体的棱长为a,所以C1O2+EO2=C1E2,所以C1O⊥OE,所以∠C1OE=90°．所以平面C1BD⊥平面BDE．2212222126COa(a)a,22a23EO()(a)a,22213CE(2a)(a)a,22则课堂小结1.判定面面垂直的两种方法①定义法②根据面面垂直的判定定理2.转化思想线线垂直线面垂直面面垂直作业二.预习课本P70~72《直线与平面垂直的性质》《平面与平面垂直的性质》一.高效学习作业本P108..如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A、B的任意一点.求证：平面PAC⊥平面PBC.APBOC证明:设已知⊙O平面为α,,BCPA.BCPA为圆的直径ABBCACAACPA且PACACPACPA面面,PACBC面,PBCBC面PBCPAC面面配用材料