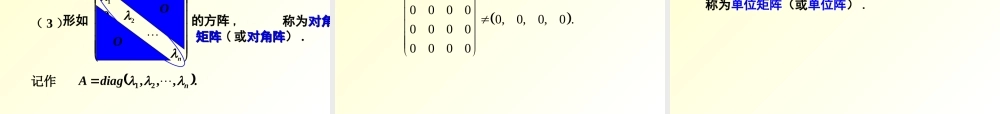高等数学--5.线性代数VIP免费

线性代数线性代数一、行列式二、矩阵三、 n 维向量四、线性方程组五、矩阵的特征值和特征向量六、二次型 把 个不同的元素排成一列，叫做这 个元素的全排列（或排列）．nn 个不同的元素的所有排列的种数用 表示，且 ． nnP!nPn 1.1. 全排列全排列一、行列式 逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列． 在一个排列 中，若数 ，则称这两个数组成一个逆序．nstiiiii21stii  一个排列中所有逆序的总数称为此排列的逆序数．2.2. 逆序数逆序数例 1 计算下列排列的逆序数，并讨论它们的奇偶性 .217986354解453689712544310010t18此排列为偶排列 .540100134 nnnpppppptnnnnnnaaaaaaaaaaaaD2121212122221112111 3. n3. n 阶行列式的定义阶行列式的定义.,,2,1;;,,2,12121列取和的所有排表示对个排列的逆序数为这的一个排列为自然数其中ntnppppppnn.094321112xx求解方程例例 22解解方程左端1229184322xxxxD,652xx解得由052xx3.2xx或. ,)()4.,)()3.),()2.DD,1)T乘此行列式等于用数一数中所有的元素都乘以同列行列式的某一行等于零则此行列式完全相同列如果行列式有两行行列式变号列互换行列式的两行即式相等行列式与它的转置行列kk4. 4. nn 阶行列式的性质阶行列式的性质., )( , )( )8., )( )7., )( )6. )( )5行列式的值不变对应的元素上去行后加到另一列然的各元素乘以同一数行把行列式的某一列式之和此行列式等于两个行列则的元素都是两数之和行若行列式的某一列式为零则此行列元素成比例列行列式中如果有两行提到行列式符号的外面以的所有元素的公因子可列行列式中某一行例 3 计算 阶行列式nabbbbabbbbabbbbaD解abbbnababbnabbabnabbbbna1111D将第 都加到第一列得n,,3,2abbbabbbabbbbna1111)1( babababbbbna1)1(00.)()1(1nbabna１）余子式与代数余子式.,)1(1 的代数余子式叫做元素；记的余子式，记作阶行列式叫做元素列划去后，留下来的行和第所在的第阶行列式中，把元素在aAMAManjianijijijjiijijijij5.5. 行列式按行（列）展开行列式按行（列）展开２）关于代数余子式的重要性质...