线面角面面角VIP免费

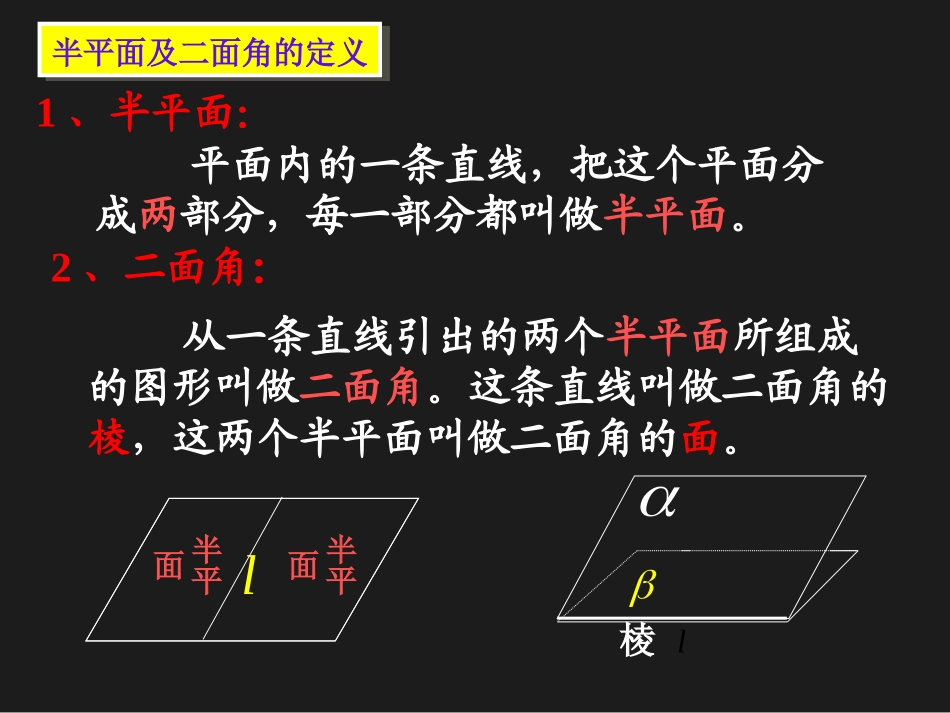
平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个这条直线和这个平面所成的角平面所成的角。一条直线垂直于平面，它们所成的角是所成的角是直角直角；一条直线和平面平行，或在平面内，它们所成的角是所成的角是00的角的角。直线和平面所成角的范围是[0[0，，9090]]。1、平面的斜线和平面所成的角例例例例例例例例ABCD－A1B1C1D1中，求AD1和平面A1D1CB所成的角。例例例例例AD1在平面A1D1CB内的射影。例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例A1D1C1B1ABCDO112OAAD0130.ADO平面内的一条直线，把这个平面分成两部分，每一部分都叫做半平面。从一条直线引出的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱，这两个半平面叫做二面角的面。1、半平面：2、二面角：半平面及二面角的定义l棱半平面半平面l2、二面角的记法：面1－棱－面2（1）、以直线为棱，以为半平面的二面角记为：ll,（2）、以直线AB为棱，以为半平面的二面角记为：,ABlAB二面角的画法与记法角BAO边边顶点从一点出发的两条射线所组成的图形叫做角。定义构成边—点—边（顶点）表示法∠AOB二面角AB面面棱a从一条直线出发的两个半平面所组成的图形叫做二面角。面—直线—面（棱）二面角—l—或二面角—AB—图形角与二面角的比较注意二面角的平面角必须满足：3）角的边都要垂直于二面角的棱1）角的顶点在棱上2）角的两边分别在两个面内以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。10lOABAOB思考:OOABABAOB=BOA等角定理：如果一个角的两边和另一个角的两边分别平行，并且方向相同，那么这两个角相等。注:（1）二面角的平面角与点的位置无关，只与二面角的张角大小有关。（2）二面角是用它的平面角来度量的，一个二面角的平面角多大，就说这个二面角是多少度的二面角。（3）平面角是直角的二面角叫做直二面角。（4）二面角的取值范围一般规定为（0,π）。二面角的平面角的定义、范围及作法l的大小与点O在L上的位置有关吗?为什么?AOB二面角的计算：1、找到或作出二面角的平面角2、证明此平面角就是所求的角3、计算出此角的大小一“作”二“证”三“计算”161、如图，AB是圆的直径，PA垂直圆所在的平面，C是圆上任一点，则二面角P-BC-A的平面角为:A.ABP∠B.ACP∠C.都不是基础基础练习练习2、已知P为二面角内一点，且P到两个半平面的距离都等于P到棱的距离的一半，则这个二面角的度数是多少？pαβιABOABCP60º二面角OABPC取AB的中点为E，连PE，OE∵O为AC中点，∠ABC=90º∴OE∥BC且OEBC212221在Rt△POE中，OE，PO2tan2PEO∴22∴所求的二面角P-AB-C的正切值为3．如图，三棱锥P-ABC的顶点P在底面ABC上的射影是底面Rt△ABC斜边AC的中点O，若PB=AB=1，BC=，求二面角P-AB-C的正切值。∴∠PEO为二面角P-AB-C的平面角OE⊥AB，因此PE⊥ABE解：223在Rt△PBE中，BE，PB=1，PE21线段MN长6，M到平面β的距离是1，N到平面β的距离是4，求MN与平面β所成角的余弦值。βMNM'N'O∠MOM'就是MN与平面β所成的角移出图MNN'M'O614解：当M，N在平面同则时有164OMOMOM=2'1sin2MOM'3cos.2MOM如图，已知P是二面角α-AB-β棱上一点，过P分别在α、β内引射线PM、PN，且∠MPN=60º∠BPM=∠BPN=45º，求此二面角的度数。βαABPMNCDO解：在PB上取不同于P的一点O，在α内过O作OC⊥AB交PM于C，在β内作OD⊥AB交PN于D，连CD，可得∠COD是二面角α-AB-β的平面角设PO=a，∵∠BPM=∠BPN=45º∴CO=a，DO=a，PCa，PDa22又∵∠MPN=60º∴CD=PCa2∴∠COD=90º因此，二面角的度数为90ºaOPC二面角