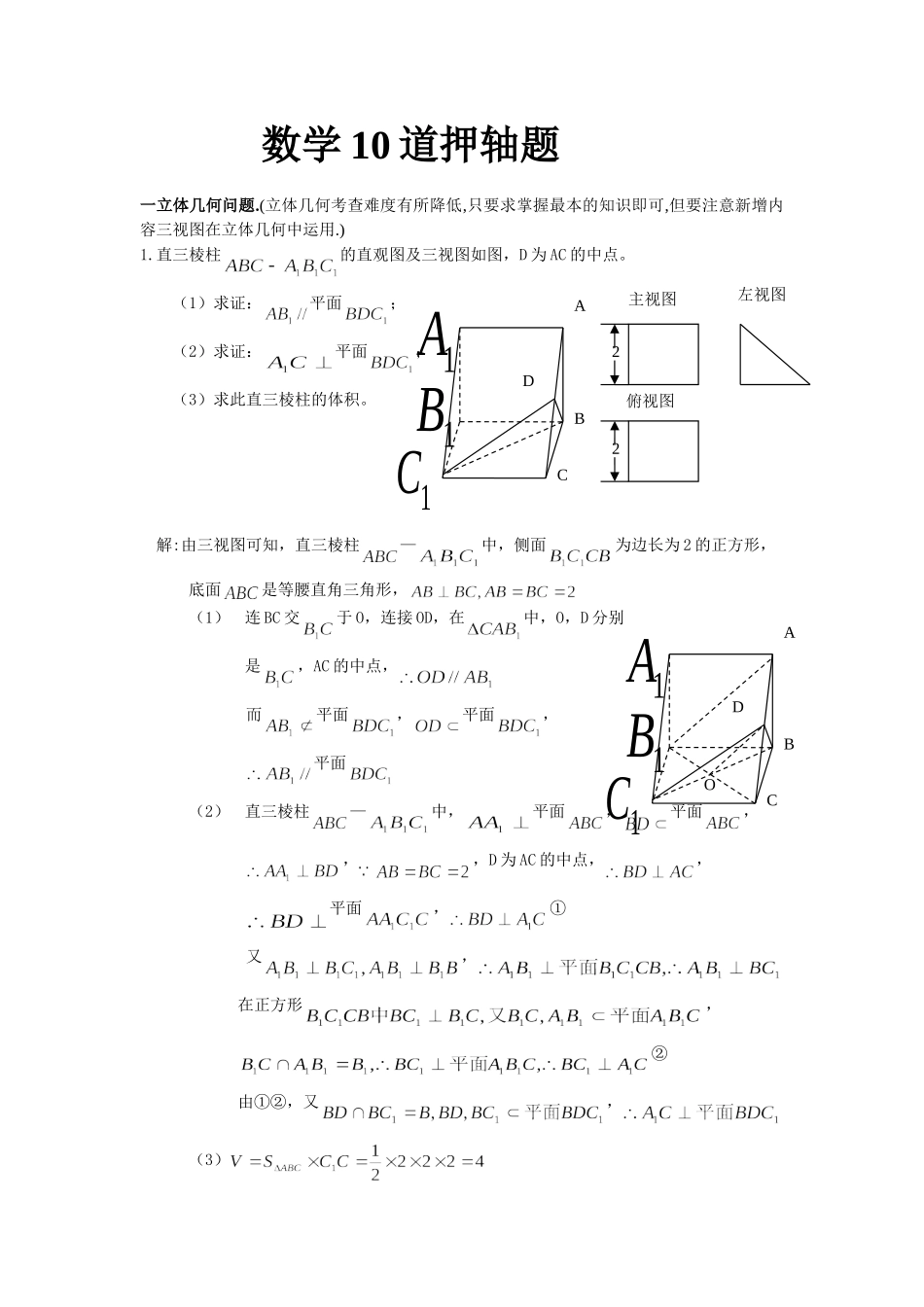
数学 10 道押轴题 一立体几何问题.(立体几何考查难度有所降低,只要求掌握最本的知识即可,但要注意新增内容三视图在立体几何中运用.)1.直三棱柱的直观图及三视图如图,D 为 AC 的中点。(1)求证:平面;(2)求证:平面;(3)求此直三棱柱的体积。解:由三视图可知,直三棱柱—中,侧面为边长为 2 的正方形,底面是等腰直角三角形,(1)连 BC 交于 O,连接 OD,在中,O,D 分别是,AC 的中点, 而平面,平面, 平面(2)直三棱柱—中,平面,平面, ,,D 为 AC 的中点,, 平面,① 又, 在正方形,② 由①②,又,(3)ABCD1A1B1C22主视图左视图俯视图ABCD1A1B1CO二解析几何问题(估计解析考查的热点问题应为椭圆和圆,由于圆为新增内容,故选编两道与圆相关的问题)1. 已知过点,且方向向量的直线 与圆,相交于两点。(1)求实数 的取值范围;(2)求证:是定值。(3)若为坐标原点,且,求 的值。解:(1)连接 OP,Q 为切点,PQ OQ,由勾股定理得,又由已知PQ=PA,故,即,化简得1. 由,得,PQ= ,故当时,PQ=,即线段 PQ 长的最小值为。2. 设圆 P 的半径为 R,圆 P 与圆 O 有公共点,圆 O 的半径为 1, ,即,且,而 , 故当时,PQ 的最小值为,此时, 得半径最小值圆 P 方程为2.已知圆,设点是直线上两点,它们的横坐标分别是,点 P 在线段 BC 上,过点 P 作圆 M 的切线 PA,切点为 A。(1)若,求直线 PA 的方程;(2)若 O 为原点,经过 A,P,M 三点的圆心是 D,求线段 DO 长的最小值解:(1)设解得或(舍去),,由题意知切线 PA 的斜率存在,设斜率为 ,所以 PA 的直线方程为:,即PA 与圆 M 相切,,解得或所以 PA 的直线方程是或(2),与圆 M 相切于点 A,,经过 A,P,M 三点的圆心 D 是线段 MP 的中点, 的坐标是,设, (1)当,即时,(2)当,即时,(3),即时, 故三:函数问题(函数是考查的热点问题,几个基本函数如二次函数,对数函数等将是考查重点)1 已知二次函数和一次函数,其中且满足,;(1)证明:函数与的图象交于不同的两点;(2)若函数在上的最小值为 ,最大值为,试求的值。解:(1)由与得,因为所以从而即函数与的图象交于不同的两点(2)设 由(1)知,又, 即,由此知函数在上为增函数由解得2.函数是定义在 R 上的偶函数,且对任意实数 都有成立。当时,(1)求当时,函数的表达式;(2)求当时,函数...