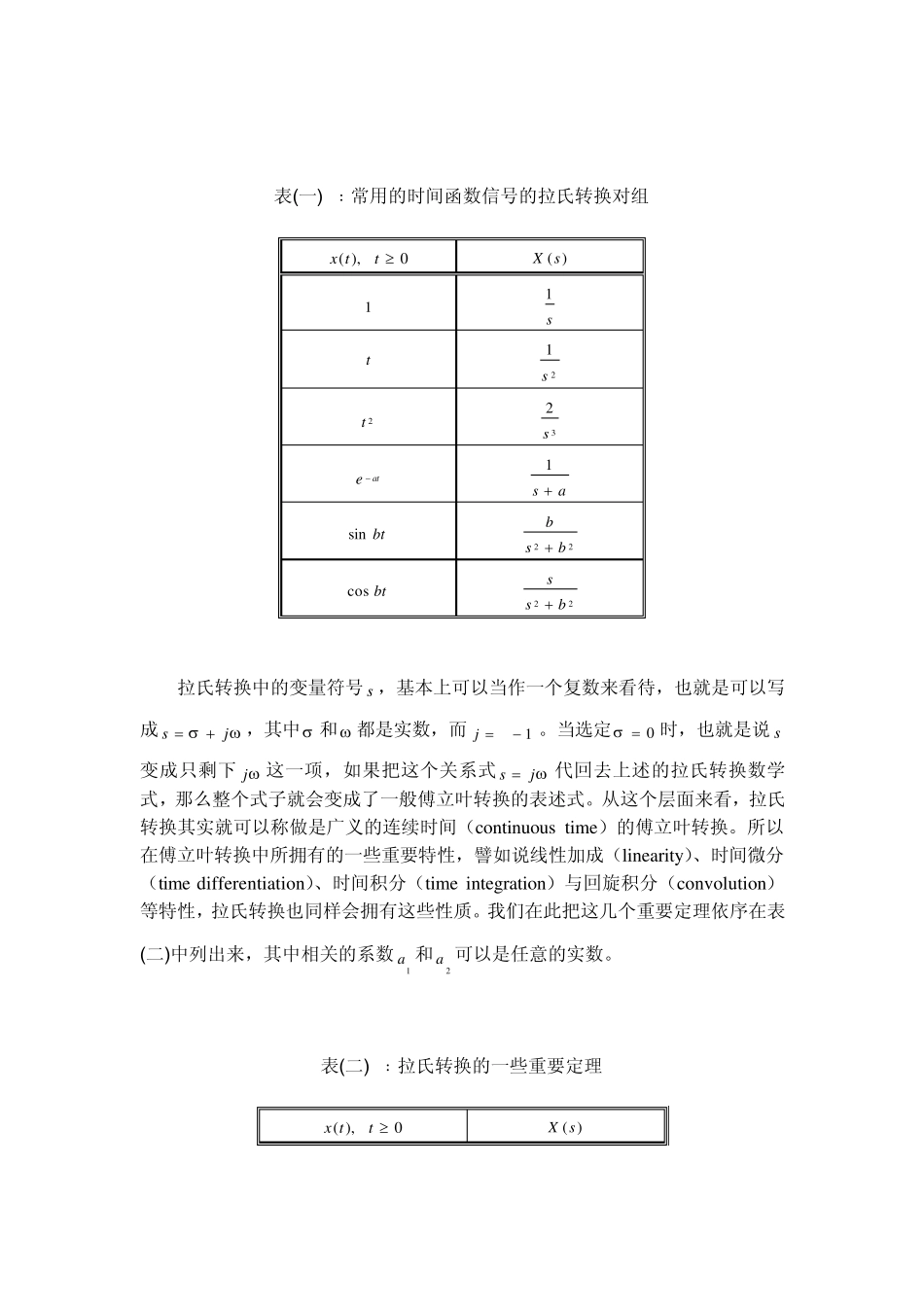
拉普拉斯转换(Laplace Transform) 通常来说,一般我们日常生活中所接触到的信号,大都是以时间的函数来表示,因为这具有一般人可以理解的物理上直观的意义。可是因为信号在系统中相关的分析与应用上的需要,常常就必须使用其它的方式来表示这些信号。之前,在本电子报中所提到的傅立叶转换(Fourier transform),就是以频率的形式来表示信号的有效方法。在这篇文章中,我们将介绍另一种表示信号的方式,那就是十八世纪法国著名数学家拉普拉斯(Pierre Simon de Laplace)在他的著作“Theorie analytique des probabilities”中所提出的拉普拉斯转换(Laplace transform)(以下简称为拉氏转换)。在拉氏转换相对应的空间领域里,通常惯用以变量符号s 的函数来作为信号的表述。而在事实上,由于拉氏转换拥有一对一的对应特性,因此并不会造成信号转换之间的混淆。换句话说,一个以时间函数)(tx所表示的信号,就只会有一个与其相对应的拉氏转换表述函数)(sX,但是特别要注意的是,并非所有的时间信号都会存在有与其相对应的拉氏转换。一般在拉氏转换的定义上,我们会有下列数学积分运算的关系式﹕ 0)()}({)(dtetxtxsXstL 此外,我们也会把下列表述的关系式称做为一组拉氏转换对组(Laplace transform pair)﹕ )}({)()()}({1sXtxsXtxLL 其中符号}{L表示的是拉氏转换的积分运算,而符号}{1 L被称做反拉氏转换(inverse Laplace transform),也就是拉氏转换的逆运算。 举例来说,当时间函数1)(tx的时候,其相对应的拉氏转换经过上述计算后,就可以被表示成ssX1)(;而当信号被选为一个指数函数的形式时,也就是tetx)(,它的拉氏转换就可以经计算而被写成11)(ssX。为了拉氏转换在使用上的方便,一些常用的时间函数信号的拉式转换,都可以直接从登载有拉式转换对组的转换表上查得。表(一)列出了一些常用的时间函数信号的拉氏转换对组,其中相关的系数a 和 b 可以是任意的实数。 表(一) ﹕常用的时间函数信号的拉氏转换对组 0),(ttx )(sX 1 s1 t 21s 2t 32s ate as 1 btsin 22bsb btcos 22bss 拉氏转换中的变量符号s ,基本上可以当作一个复数来看待,也就是可以写成js,其中 和 都是实数,而 1j。当选定0时,也就是说s变成只剩下j这一项,如果把这个关系式js 代回去上述的拉氏转换数学式,那么整个式子就会变成了一般傅立叶...