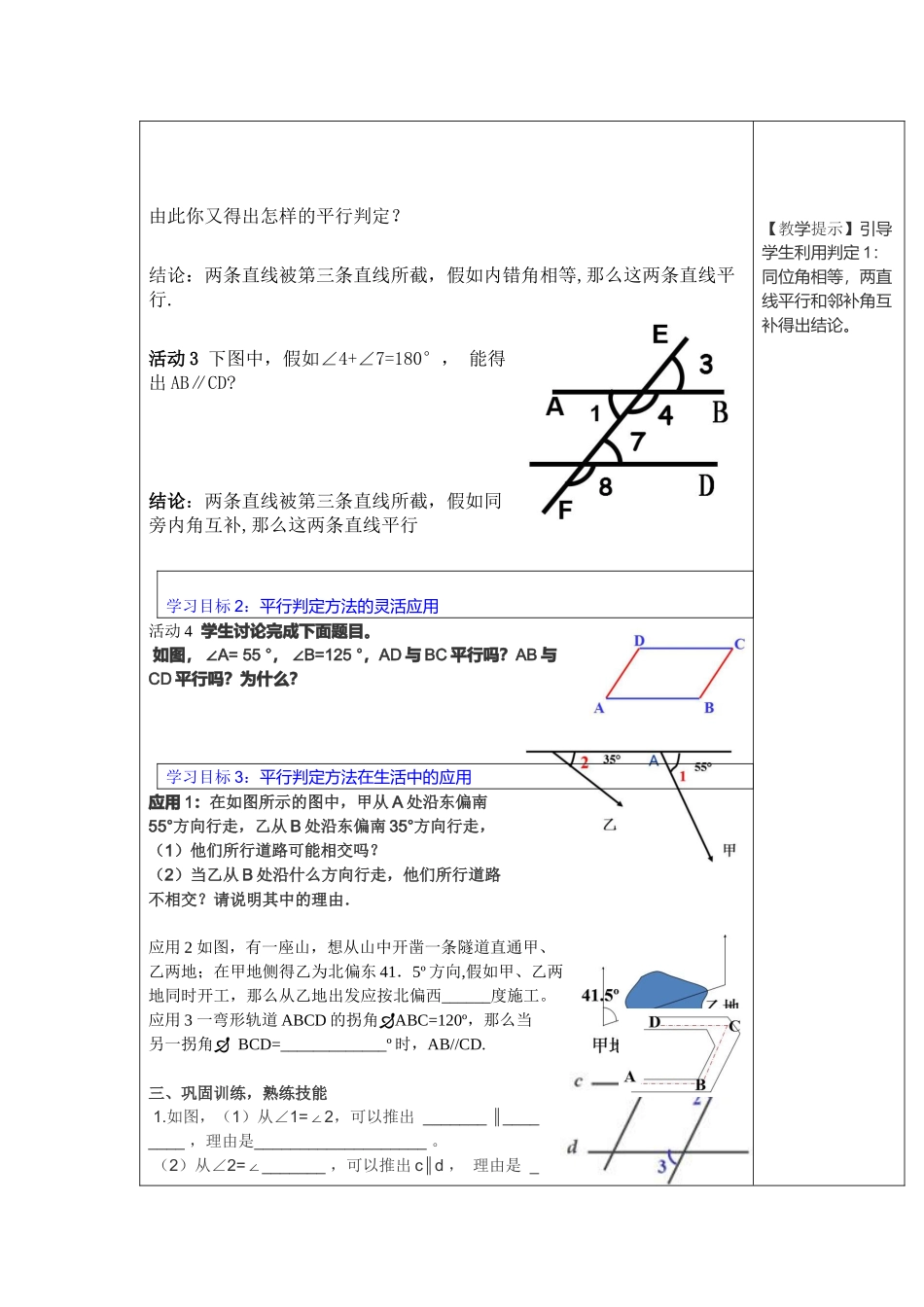
第 1 课时 平行线的判定教学目标 1、通过操作、观察、想象、推理、沟通等活动推演出平行线的判定方法; 2、会运用转化的思想将新问题转化为已知或者已解决的问题,体会数学的转化思维; 3、会运用数学语言描述并证明平行线的判定方法,认识证明的必要性和证明过程的严密性,深刻理解直线平行的判定方法; 4、灵活应用判定方法进行直线是否平行或者其它结论的推理推断。重点:理解线平行的判定方法,并会根据判定方法进行简单的推理应用。难点:平行线判定方法的灵活运用和其推导过程中的转化思想的认识。教学过程 一、创设情境,引入课题 一个长方形工件,假如需要检验它是否符合设计要求,除了度量它的长和宽的尺寸外,还要检查各面的长宽是否分别平行,而这些实际问题假如根据平行线的定义去推断是不可能的,但又如何推断它们是否平行呢?二、目标导学,探究新知 目标导学 1:平行的判定方法活动 1:如图,三根木条相交成∠1, ∠2,固定木条 b、c,转动木条 a , 观察∠1, ∠2 满足什么条件时直线 a 与 b 平行。 直线 a 和 b 不平行 直线 a∥b得出结论:两条直线被第三条直线所截,假如同位角相等,那么这两条直线平行.活动 2 图中,假如∠1=∠7,能得出 AB∥CD 吗?写出你的推理过程。【教学备注】【老师提示】引导学生去发现,两直线之所以平行,是因为同位角相等,进而引导学生用文字述叙概括出判定两直线平行的方法。【老师提示】引导学生利用判定 1:同位角相等,两直线平行和对顶角相等得出结论。由此你又得出怎样的平行判定?结论:两条直线被第三条直线所截,假如内错角相等,那么这两条直线平行.活动 3 下图中,假如∠4+∠7=180°, 能得出 AB∥CD?结论:两条直线被第三条直线所截,假如同旁内角互补,那么这两条直线平行学习目标 2:平行判定方法的灵活应用活动 4 学生讨论完成下面题目。 如图, ∠A= 55 ° , ∠B=125 °,AD 与 BC 平行吗?AB 与CD 平行吗?为什么?学习目标 3:平行判定方法在生活中的应用应用 1:在如图所示的图中,甲从 A 处沿东偏南55°方向行走,乙从 B 处沿东偏南 35°方向行走,(1)他们所行道路可能相交吗?(2)当乙从 B 处沿什么方向行走,他们所行道路不相交?请说明其中的理由.应用 2 如图,有一座山,想从山中开凿一条隧道直通甲、乙两地;在甲地侧得乙为北偏东 41.5º 方向,假如甲、乙两地同时开工,那么从乙地出发应按北偏西____...