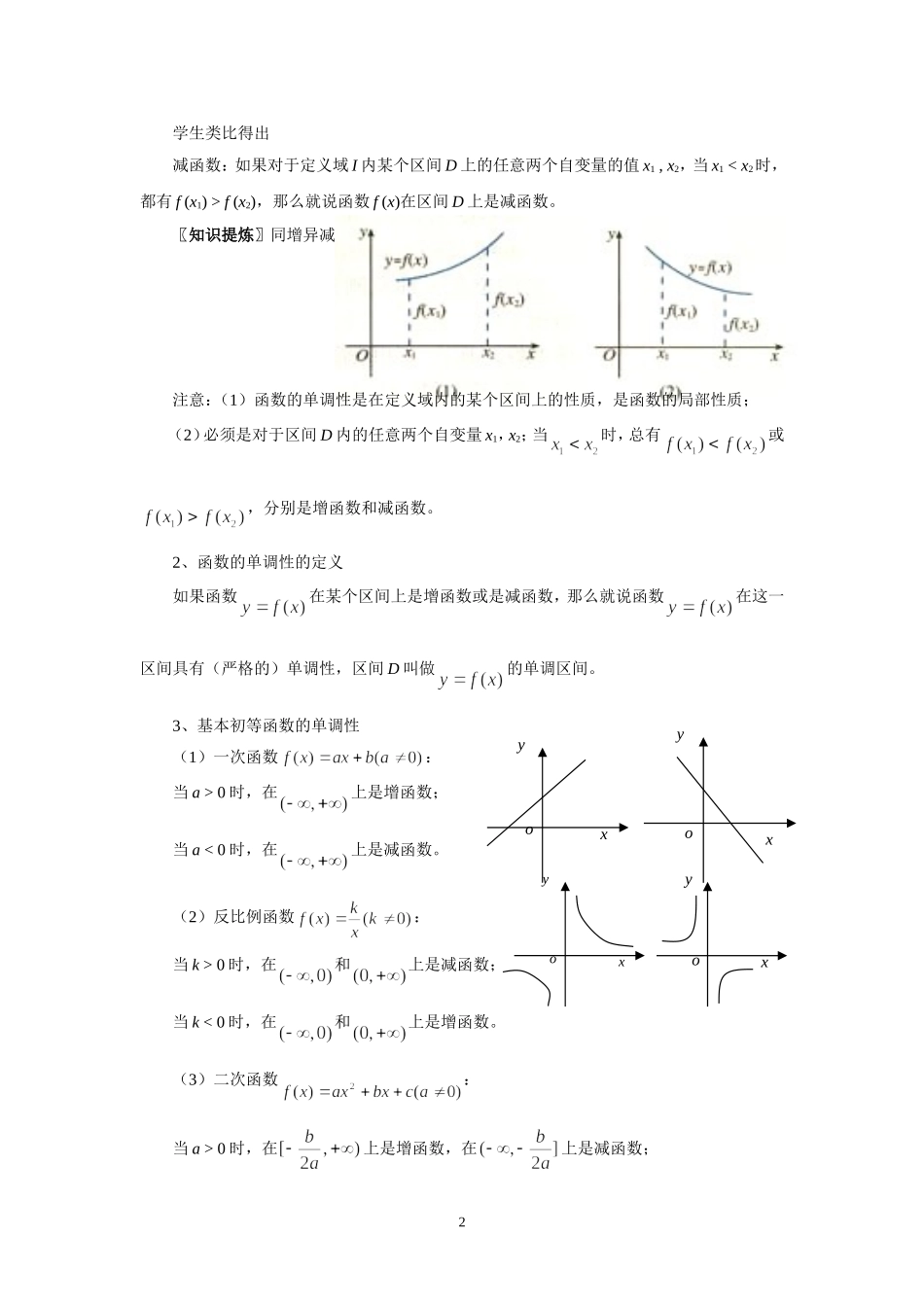
1.3 函数的基本性质1.3.1 单调性与最大(小)值第一课时 函数的单调性三维目标定向〖知识与技能〗(1)结合具体函数,理解函数的单调性及其几何意义;(2)能利用函数图象理解和研究函数的单调性;(3)能利用定义判定一些简单函数的单调性。〖过程与方法〗借助二次函数体验单调性概念的形成过程,领会数形结合的数学思想,学会运用概念进行判断推理,养成细心观察,严谨论证的良好思维习惯。〖情感、态度与价值观〗渗透由具体到抽象的认识,通过合作交流,培养学生反思学习、善于思考的习惯。教学重难点〖重点〗函数单调性的概念。〖难点〗熟练运用定义判断、证明函数的单调性。教学过程设计一、问题情境设疑引例:画出一次函数和二次函数的图象。(几何画板)问题:以上两个图象有什么特征?——“上升”、“下降”上升:随着 x 的增大,相应的 f (x)也增大;下降:随着 x 的增大,相应的 f (x)减小。二、核心内容整合1、函数的单调性的概念:问题:如何用数学语言描述“随着 x 的增大,相应的 f (x)也增大”?——学生探究。增函数:如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 x1 , x2,当 x1 < x2时,都有 f (x1) < f (x2),那么就说函数 f (x)在区间 D 上是增函数。1学生类比得出减函数:如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 x1 , x2,当 x1 < x2时,都有 f (x1) > f (x2),那么就说函数 f (x)在区间 D 上是减函数。〖知识提炼〗同增异减注意:(1)函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;(2)必须是对于区间 D 内的任意两个自变量 x1,x2;当时,总有或,分别是增函数和减函数。2、函数的单调性的定义如果函数在某个区间上是增函数或是减函数,那么就说函数在这一区间具有(严格的)单调性,区间 D 叫做的单调区间。3、基本初等函数的单调性(1)一次函数:当 a > 0 时,在上是增函数;当 a < 0 时,在上是减函数。(2)反比例函数:当 k > 0 时,在和上是减函数;当 k < 0 时,在和上是增函数。(3)二次函数:当 a > 0 时,在上是增函数,在上是减函数;2yoxyoxoyxyox当 a < 0 时,在上是减函数,在上是增函数;三、例题分析示例例 1、如图是定义在区间[– 5,5]上的函数,根据图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?例 2、物理学中的玻意耳定律(k 为正...