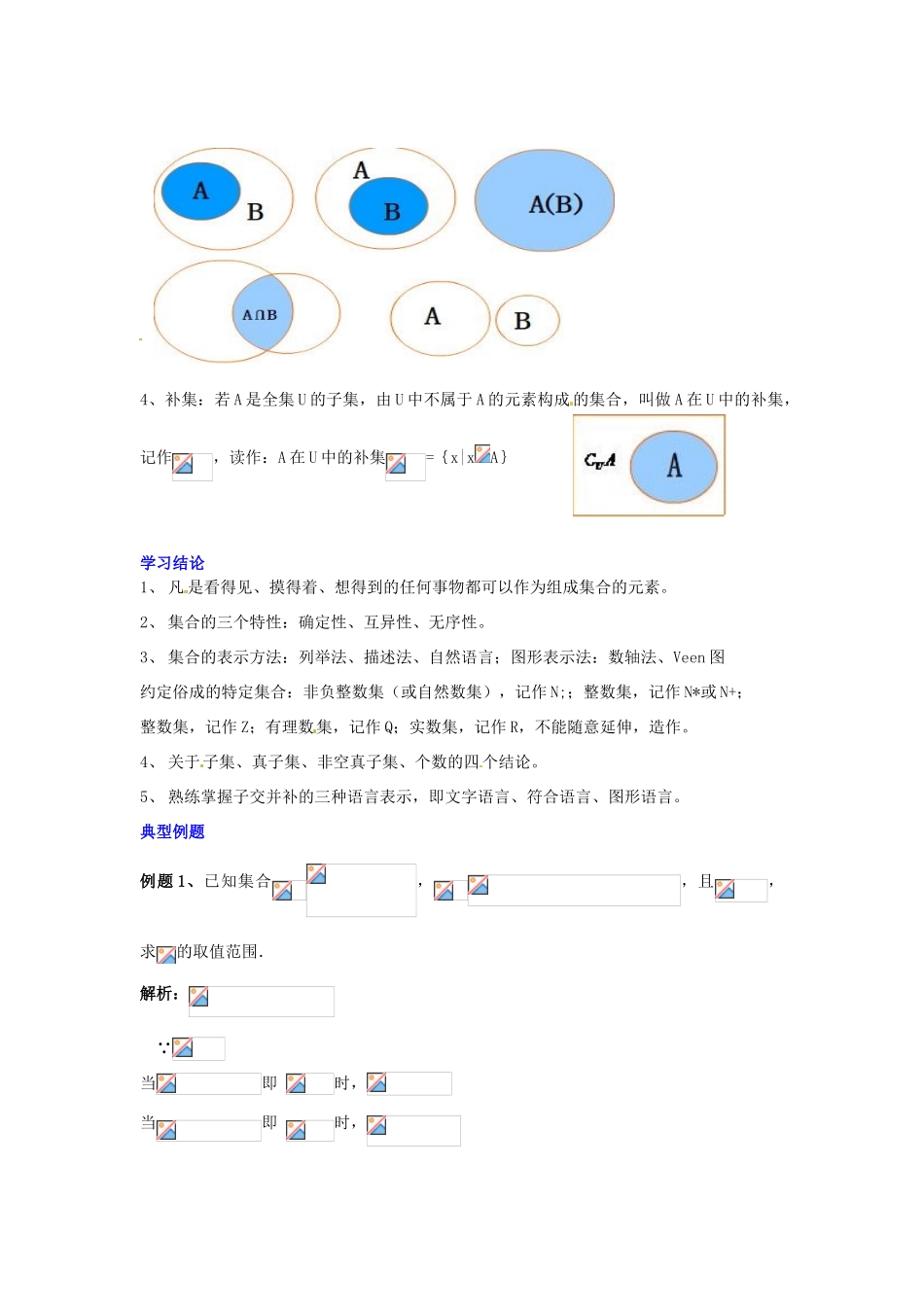
集合学习过程知识点 1:集合与元素的理解(1)一般地,研究对象统称为元素,常用 a,b,c…表示,一些元素组成的总体叫集合,常用 A,B,C…表示,也简称集,如果 a 是集合 A 的元素,就说 a 属于 A,记作 a∈A,如果 a不是集合 A 的元素,就说 a 不属于 A,记作 aA。(2)注意凡是看得见、摸得着、想得到的任何事物都可以作为组成集合的对象。(3)集合是一个整体已经暗含所有、全部、全体的意思,因此一些对象一旦组成了集合,那么这个集合就是这些对象的全体,而非个别对象,例如{x|x>0}就是指所有大于 0 的实数。(4)集合与元素之间的关系是整体与个体的关系这种写法是错误的{1}∈{1、2、3}。知识点 2:集合中元素的三个特性(1)确定性:设 A 是一个给定的集合 ,x 是某一个具体对象,则或者是 A 的元素,或者不是 A 的元素,两种情况必有一种且只有一种成立。(2)互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素。(3)无序性:{a,b,c}与{b,a,c}是同一个集合。知识点 3:集合的表示方法(1)列举法:把集合中的元素一一列举出来,写在大括号 内表示集合的方法。一般有这样几种不同的写法{1,2,3,4},{1,2,3,…,100},{1,2,3,4,…,n,…}(2)描述法:{x|x∈p(x)},其中一对大括号是必须的,x 是代表元素,他说明这个集合是点集还是数集等,p(x)是代表元素满足的性质。竖线不可省。(3)自然语言:如{2,4,6,8}用自然语言叙述为:大于等于 2 且小于等于 8 的偶数组成的集合。(4)集合的图形表示法:1、韦恩(Venn)图,用平面上封闭曲线的内部表示集合2、数轴法,如下表示集合{x|-4