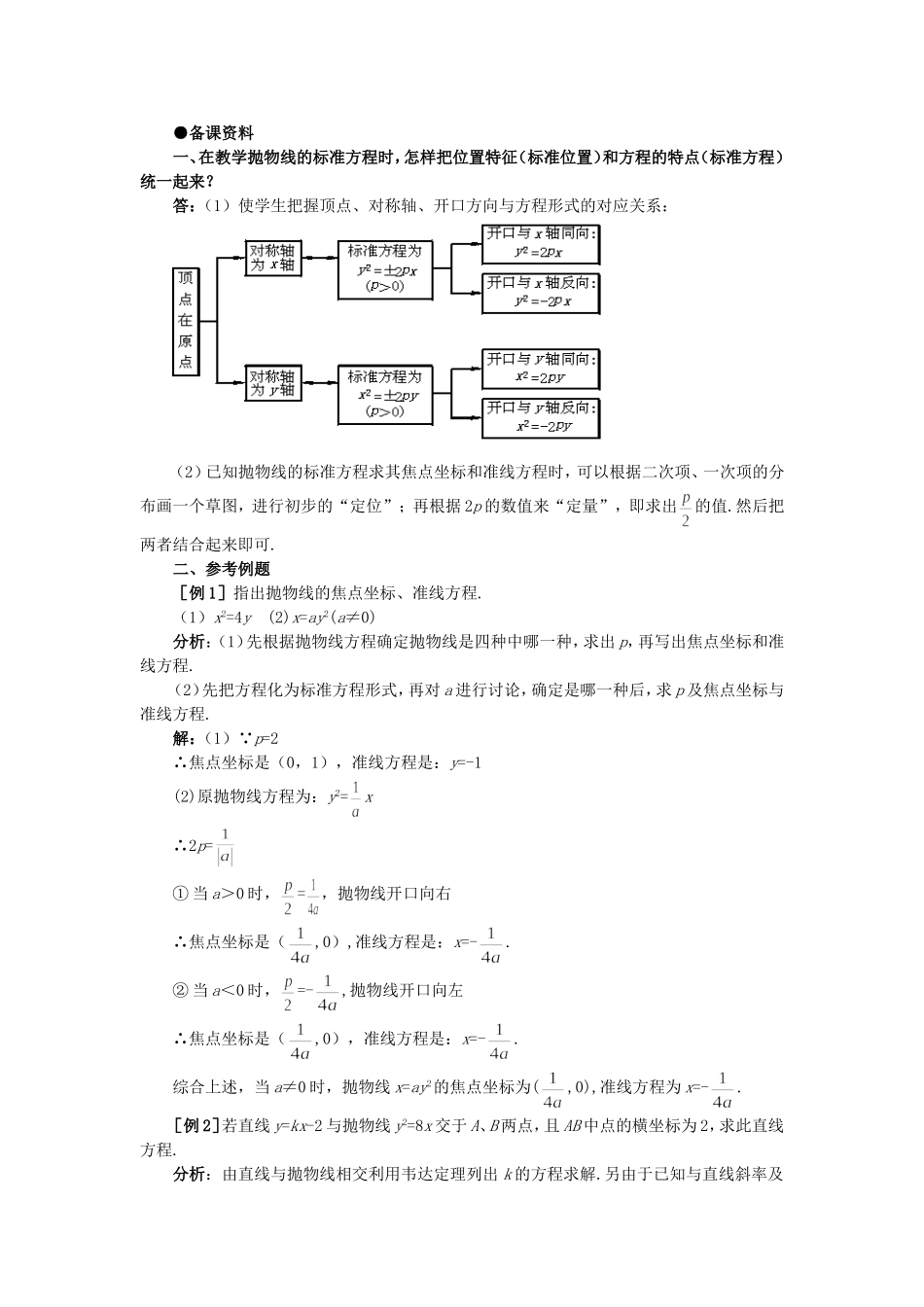
●备课资料一、在教学抛物线的标准方程时,怎样把位置特征(标准位置)和方程的特点(标准方程)统一起来?答:(1)使学生把握顶点、对称轴、开口方向与方程形式的对应关系: (2)已知抛物线的标准方程求其焦点坐标和准线方程时,可以根据二次项、一次项的分布画一个草图,进行初步的“定位”;再根据 2p 的数值来“定量”,即求出的值.然后把两者结合起来即可.二、参考例题[例 1]指出抛物线的焦点坐标、准线方程.(1)x2=4y (2)x=ay2(a≠0)分析:(1)先根据抛物线方程确定抛物线是四种中哪一种,求出 p,再写出焦点坐标和准线方程.(2)先把方程化为标准方程形式,再对 a 进行讨论,确定是哪一种后,求 p 及焦点坐标与准线方程.解:(1) p=2∴焦点坐标是(0,1),准线方程是:y=-1(2)原抛物线方程为:y2=x∴2p=① 当 a>0 时,=,抛物线开口向右∴焦点坐标是(,0),准线方程是:x=-.② 当 a<0 时,=-,抛物线开口向左∴焦点坐标是(,0),准线方程是:x=-.综合上述,当 a≠0 时,抛物线 x=ay2的焦点坐标为(,0),准线方程为 x=-.[例 2]若直线 y=kx-2 与抛物线 y2=8x 交于 A、B 两点,且 AB 中点的横坐标为 2,求此直线方程.分析:由直线与抛物线相交利用韦达定理列出 k 的方程求解.另由于已知与直线斜率及弦中点坐标有关,故也可利用“作差法”求 k.解法一:设 A(x1,y1)、B(x2,y2),则由可得:k2x2-(4k+8)x+4=0 直线与抛物线相交∴k≠0 且 Δ>0则 k>-1 AB 中点横坐标为∴解得:k=2 或 k=-1(舍去)故所求直线方程为:y=2x-2解法二:设 A(x1,y1),B(x2,y2)则有 y12=8x1 y22=8x2两式作差解:(y1-y2)(y1+y2)=8(x1-x2)即 x1+x2=4∴y1+y2=kx1-2+kx2-2=k(x1+x2)-4=4k-4∴k=故 k=2 或 k=-1(舍去)则所求直线方程为:y=2x-2[例 3]求证:以抛物线的焦点弦为直径的圆心与抛物线的准线相切.分析:可设抛物线方程为 y2=2px(p>0).如图所示,只须证明=|MM1|,则以 AB 为直径的圆,必与抛物线准线相切.证明:作 AA1⊥l 于 A1,BB1⊥l 于 B1.M 为 AB 中点,作 MM1⊥l 于 M1,则由抛物线的定义可知:|AA1|=|AF|,|BB1|=|BF|在直角梯形 BB1A1A 中:|MM1|=(|AA1|+|BB1|)=(|AF|+|BF|)=|AB|∴|MM1|=|AB|,故以 AB 为直径的圆,必与抛物线的准线相切.说明:类似有:以椭圆焦点弦为直径的圆与相对应的准线相离;以双曲线焦点弦为直径的圆与相应的准线相交.[例 4](1)设抛物线 y2=4x...