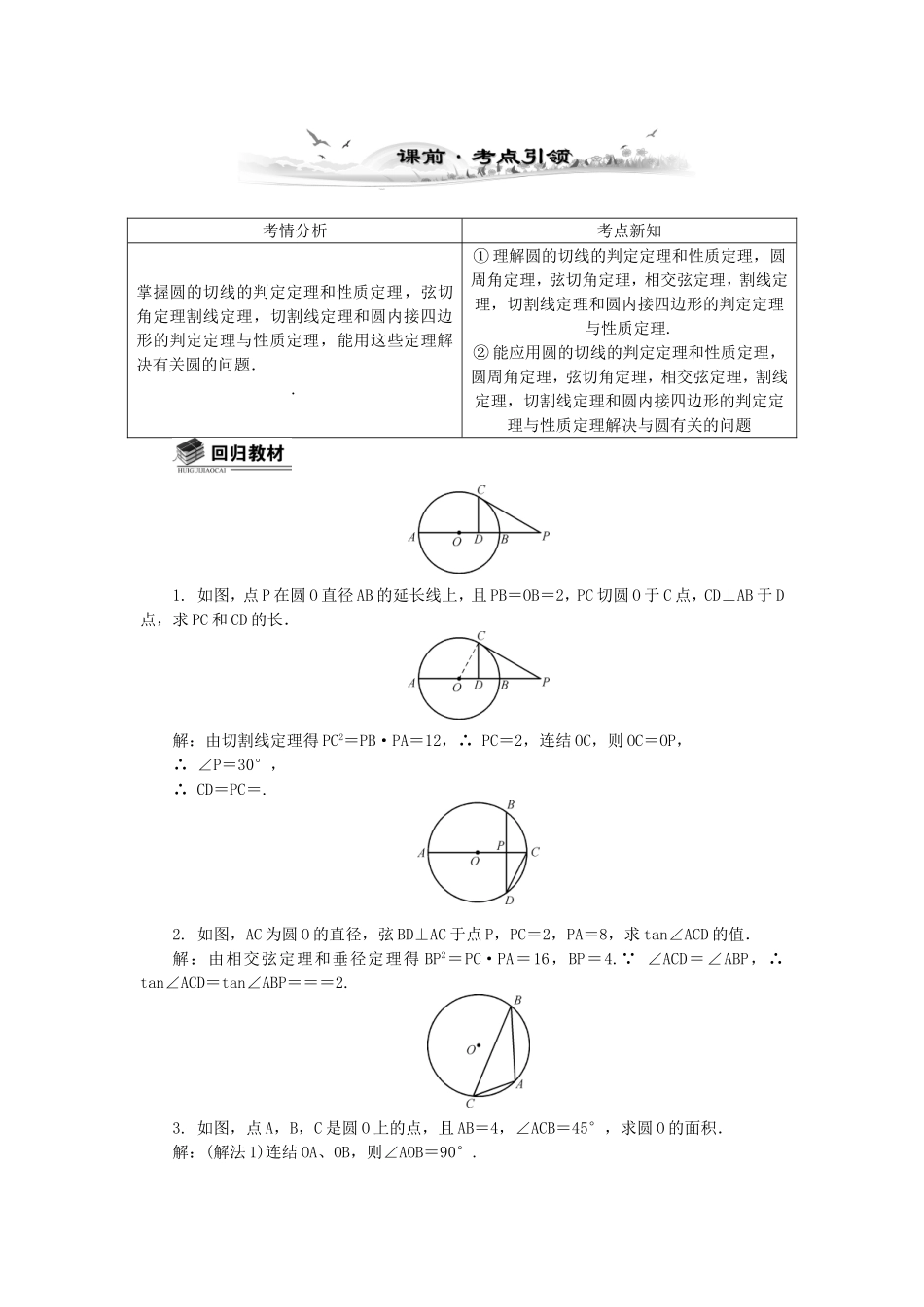
考情分析考点新知掌握圆的切线的判定定理和性质定理,弦切角定理割线定理,切割线定理和圆内接四边形的判定定理与性质定理,能用这些定理解决有关圆的问题..①理解圆的切线的判定定理和性质定理,圆周角定理,弦切角定理,相交弦定理,割线定理,切割线定理和圆内接四边形的判定定理与性质定理.②能应用圆的切线的判定定理和性质定理,圆周角定理,弦切角定理,相交弦定理,割线定理,切割线定理和圆内接四边形的判定定理与性质定理解决与圆有关的问题1.如图,点P在圆O直径AB的延长线上,且PB=OB=2,PC切圆O于C点,CD⊥AB于D点,求PC和CD的长.解:由切割线定理得PC2=PB·PA=12,∴PC=2,连结OC,则OC=OP,∴∠P=30°,∴CD=PC=.2.如图,AC为圆O的直径,弦BD⊥AC于点P,PC=2,PA=8,求tan∠ACD的值.解:由相交弦定理和垂径定理得BP2=PC·PA=16,BP=4. ∠ACD=∠ABP,∴tan∠ACD=tan∠ABP===2.3.如图,点A,B,C是圆O上的点,且AB=4,∠ACB=45°,求圆O的面积.解:(解法1)连结OA、OB,则∠AOB=90°. AB=4,OA=OB,∴OA=2,则S圆=π×(2)2=8π.(解法2)2R==4R=2,则S圆=π×(2)2=8π.4.如图,点B在圆O上,M为直径AC上一点,BM的延长线交圆O于N,∠BNA=45°,若圆O的半径为2,OA=OM,求MN的长.解: ∠BNA=45°,∴∠BOA=90°. OM=2,BO=2,∴BM=4. BM·MN=CM·MA=(2+2)(2-2)=8,∴MN=2.5.如图,已知P是圆O外一点,PD为圆O的切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4,求圆O的半径长和∠EFD的大小.解:由切割线定理,得PD2=PE·PFPE===4EF=8,OD=4. OD⊥PD,OD=PO,∴∠P=30°,∠POD=60°,∴∠PDE=∠EFD=30°.1.圆周角定理(1)圆周角定理:圆周角的度数等于其所对弧度数的一半.(2)推论1:同弧(或等弧)上的圆周角相等.同圆或等圆中,相等的圆周角所对的弧相等.(3)半圆(或直径)上的圆周角等于90°.反之,90°的圆周角所对的弦为直径.2.圆的切线(1)圆的切线的性质与判定①切线的定义:当直线与圆有2个公共点时,直线与圆相交;当直线与圆有且只有1个公共点时,直线与圆相切,此时直线是圆的切线,公共点称为切点;当直线与圆没有公共点时,直线与圆相离.②切线的判定定理:过半径外端且与这条半径垂直的直线是圆的切线.③切线的性质定理:圆的切线垂直于经过切点的半径.④切线长定理:从圆外一点引圆的两条切线长相等.(2)弦切角①弦切角的定义:顶点在圆上,一边与圆相切,另一边与圆相交的角称为弦切角.②弦切角定理:弦切角的度数等于所夹弧的度数的一半.③推论:同弧(或等弧)上的弦切角相等,同弧(或等弧)上的弦切角与圆周角相等.3.相交弦定理相交弦定理:圆的两条相交弦,被交点分成的两段的积相等.4.切割线定理(1)割线定理:从圆外一点引圆的两条割线,这点到每条割线与圆的交点的两条线段的积相等.(2)切割线定理:从圆外一点引圆的一条割线与一条切线,切线长是这点到割线与圆的两个交点的线段的等比中项.5.圆内接四边形(1)圆内接四边形性质定理:圆内接四边形对角互补.(2)圆内接四边形判定定理:如果四边形的对角互补,则此四边形内接于圆.[备课札记]题型1探求角的关系例1如图,AB是圆O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证:∠DEA=∠DFA.证明:连结AD,因为AB为圆的直径,所以∠ADB=90°.又EF⊥AB,∠EFA=90°,所以A、D、E、F四点共圆.所以∠DEA=∠DFA.(2011·南通三模)如图,圆O的直径AB的延长线与弦CD的延长线相交于点P,E为圆O上一点,AE=AC,求证:∠PDE=∠POC.证明:因为AE=AC,AB为直径,故∠OAC=∠OCA=∠OAE.所以∠POC=∠OAC+∠OCA=∠OAC+∠OAE=∠EAC.又∠EAC=∠PDE,所以∠PDE=∠POC.题型2求线段长度例2如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.(1)求证:△DEF∽△EFA;(2)如果FG=1,求EF的长.(1)证明:因为EF∥CB,所以∠BCE=∠FED.又∠BAD=∠BCD,所以∠BAD=∠FED.又∠EFD=∠EFD,所以△DEF∽△EFA.(2)解:由(1)得=,即EF2=FA·FD.因为FG是切线,所以FG2=FD·FA,所以E...