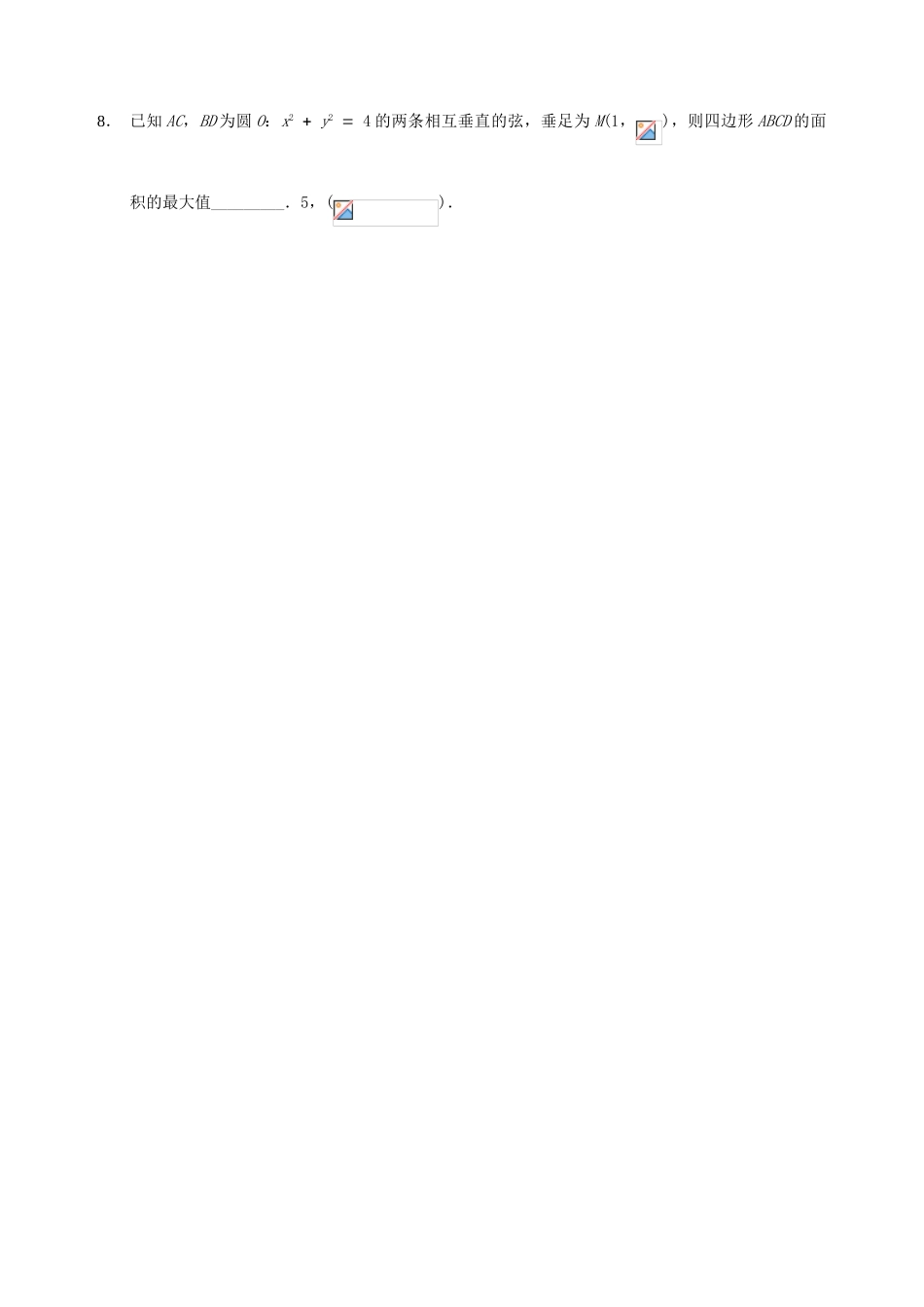
江苏省苏州市第五中学高三数学 直线与圆复习学案【考纲要求】能判断直线与圆、圆与圆的位置关系,能用直线与圆的方程解决一些简单的问题,B 级要求(圆的标准方程与一般方程为 C 级要求).主要问题:(1)判断直线与圆位置;(2)相切时会求切线方程;(3)相交时会求弦长;(4)相离时会求有关距离最值.特别关注两类问题:动中之定与最值.主要方法:数形结合法,注意利用几何性质解题.【知识梳理】1.直线与圆的位置关系:(1)相交_______;(2)相切_______;(3)相离_______.2.直线与圆相切问题:设 P(x0,y0),圆 C:x2 y2 r2 ( r 0 ).(1)若点 P 在圆 C 上,则过点 P 的圆 C 的切线方程为_________________.(2)若点 P 在圆 C 外,切线 PA ,PB 切圆于点 A,B,则直线 AB 的方程为____________.3.设直线 Ax By C 0 与圆:x2 y2 r2 ( r 0 )相交,则弦长 m ____________.【基础训练】1. 圆上一点到直线 3x 4y 2 0 的距离的最小值为________.22. 直线 l:与圆 C:的位置关系是_________.相交3. 若圆上有仅只有两个点到直线的距离等于 1,则实数 r 的取值范围是_________.(1,9)4. 由直线上的一点向圆引切线,则切线长的最小值为_______.5. 在平面直角坐 标系中,设直线 :与圆:相交于 A,B 两点,以OA,OB 为邻边作平行四边形 OAMB,若点 M 在圆上,则实数 k =_________.6. 过点 P(,1)的直线 l 与圆交于 A,B 两点,当∠ACB 最小时,直线 l 的方程为_________.2x 4y 3 0.7. 与圆 C:x2 ( y 5 )2 3 相切且在两坐标轴上截距相等的直线条数为_________.48. 已知 AC,BD 为圆 O:x2 y2 4 的两条相互垂直的弦,垂足为 M(1,),则四边形 ABCD 的面积的最大值_________.5,().【典型例题】例1 已知圆 O 的方程为 x2 y2 r2(r 为正的常数),设 P(m,n)为平面内的一个定点,求证:存在定点 Q(异于点 P),使得对圆 O 上的任意一点 M,均有为定值.例2 已知圆(0<a≤4)的圆心为 C, 直线l:y x m.(1)若 m 4,求直线 l 被圆 C 所截得弦长的最大值;(2)若直线 l 是圆 C 的切线,且直线 l 在圆心 C 的下方,当 a 在(0,4] 变化时,求 m 的取值范围....