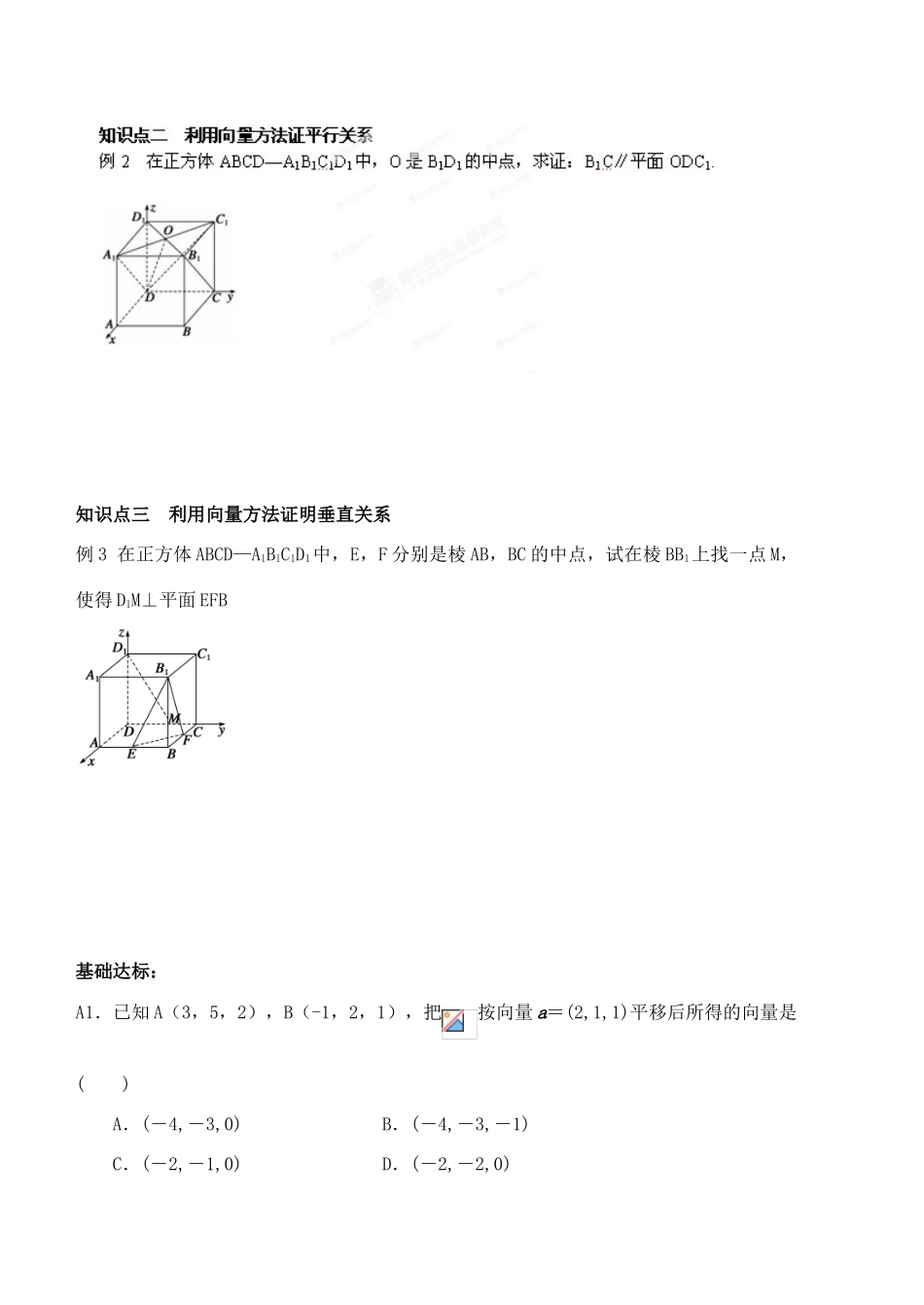
高中数学选修 2-1《立体几何中的向量方法 1》导学案姓名: 班级:_________ 组别: 组名: 【学习目标】1.会用空间向量解决立体几何中的平行问题.2.会用空间向量解决立体几何中的垂直问题.【重点】会用空间向量解决立体几何中的平行与垂直问题.【难点】会用向量语言表述线线、线面、面面的平行与垂直关系.【知识链接】若,,则1. ;2. ;3. ;4. ;5. , , ,;6. ;7. ;8. ;【学习过程】知识点一 求平面的法向量例 1 已知平面 α 经过三点 A(1,2,3),B(2,0,-1),C(3,-2,0),试求平面 α 的一个法向量.知识点三 利用向量方法证明垂直关系例 3 在正方体 ABCD—A1B1C1D1中,E,F 分别是棱 AB,BC 的中点,试在棱 BB1上找一点 M,使得 D1M⊥平面 EFB基础达标:A1.已知 A(3,5,2),B(-1,2,1),把按向量 a=(2,1,1)平移后所得的向量是( )A.(-4,-3,0) B.(-4,-3,-1)C.(-2,-1,0) D.(-2,-2,0)A2.平面 α 的一 个法向 量为(1,2,0),平面 β 的一个法向量为(2,-1,0),则平面 α与平面 β 的位置关系是( )A.平行 B.相交但不垂直C.垂直 D.不能确定B3.已知平面 α 经过点 O(0,0,0),且 e=(1,1,1)是 α 的法向量,M(x,y,z)是平面 α 内任意一点,则 x,y,z 满足的关系式是________________.C4.已知正方体 ABCD-A1B1C1D1的棱长为 2,E、F 分别是 BB1、DD1的中点,求证:(1)FC1∥平面 ADE;(2)平面 ADE∥平面 B1C1F. D5.在正棱锥 P—ABC 中,三条侧棱两两互相垂直,G 是△PAB 的重心,E、F 分别为BC、PB 上的点,且 BE∶EC=PF∶FB=1∶2.(1)求证:平面 GEF⊥平面 PBC;(2)求证:EG 是 PG 与 BC 的公垂线段.【课堂小结】1.用待定系数法求平面法向量的步骤:(1)建立适当的坐标系.(2)设平面的法向量为 n=(x,y,z).(3)求出平面内两个不共线向量的坐标 a=(a1,b1,c1),b=(a2,b2,c2).(4)根据法向量定义建立方程组.(5)解方程组,取其中一解,即得平面的法向量. 2.平行关系的常用证法,证明线面平行可转化为证直线的方向向量和平面的法向量垂直,然后说明直线在平面外,证面面平行可转化证两面的法向量平行.3.垂直关系的常用证法要证线线垂直,可以转化为对应的向量垂直.要证线面垂直,可以转化为证明这条直线与平面内两条相交直线垂直.要证面面垂直,可以转化为证明两个平面的法向量垂直.【当堂检测】A1...