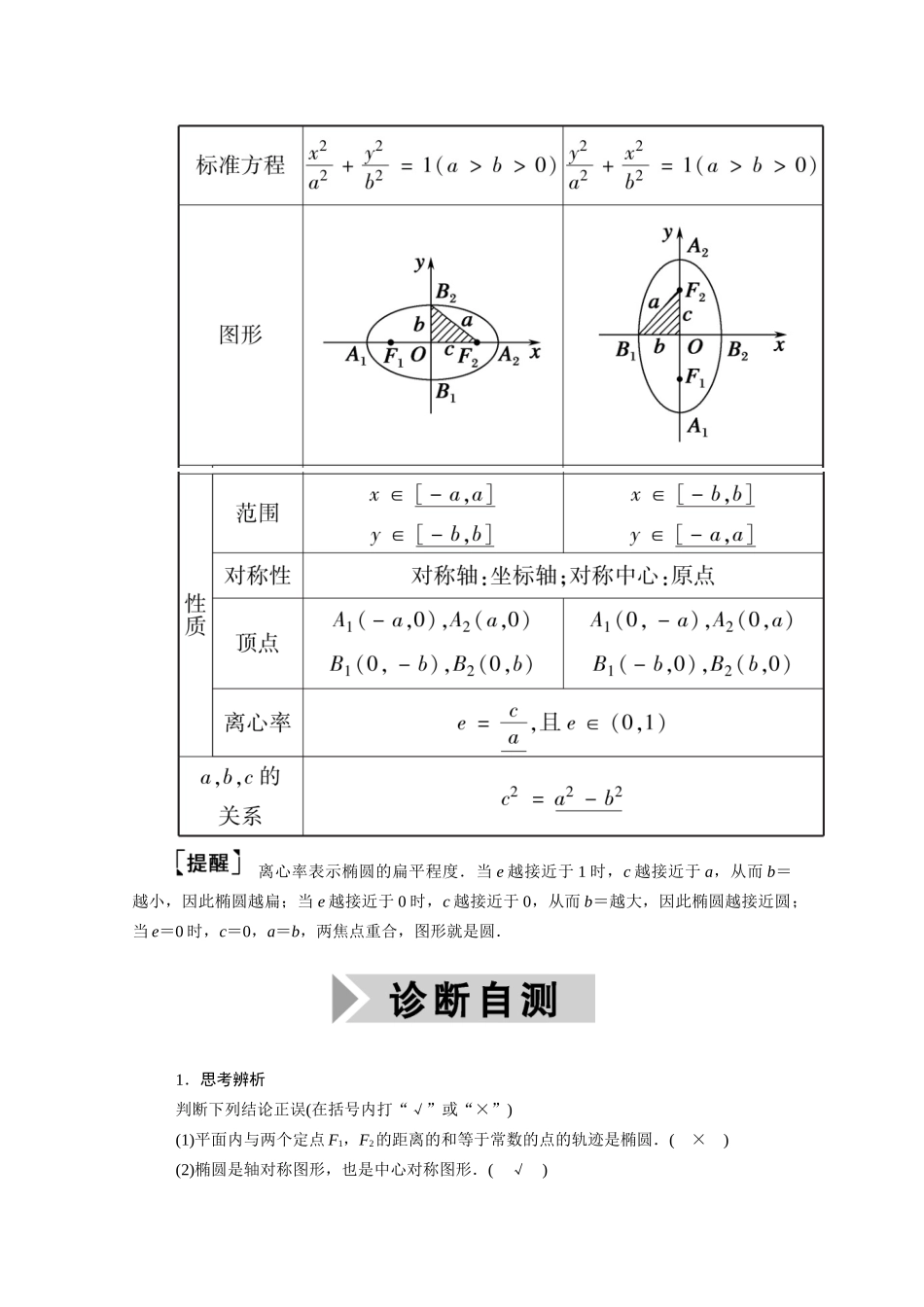
第五节 椭圆课标要求考情分析1.掌握椭圆的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率).2.了解椭圆的简单应用.3.理解数形结合的思想.1.椭圆的定义、标准方程、几何性质以及椭圆与其他知识综合应用是近几年高考命题方向方向的热点.2.常与直线、向量、三角等知识交汇考查,考查学生分析问题、解决问题的能力.3.三种题型都有可能出现,选择、填空题一般为中低档题,解答题为高档题. 知识点一 椭圆的定义平面内到两定点 F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.两定点F1,F2叫做椭圆的焦点.集合 P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中 a>0,c>0,且 a,c 为常数.(1)当 2a>|F1F2|时,M 点的轨迹是椭圆;(2)当 2a=|F1F2|时,M 点的轨迹是线段 F1F2;(3)当 2a<|F1F2|时,M 点不存在.知识点二 椭圆的标准方程和几何性质离心率表示椭圆的扁平程度.当 e 越接近于 1 时,c 越接近于 a,从而 b=越小,因此椭圆越扁;当 e 越接近于 0 时,c 越接近于 0,从而 b=越大,因此椭圆越接近圆;当 e=0 时,c=0,a=b,两焦点重合,图形就是圆.1.思考辨析判断下列结论正误(在括号内打“√”或“×”)(1)平面内与两个定点 F1,F2的距离的和等于常数的点的轨迹是椭圆.( × )(2)椭圆是轴对称图形,也是中心对称图形.( √ )(3)椭圆的离心率 e 越大,椭圆就越圆.( × )(4)方程 mx2+ny2=1(m>0,n>0,m≠n)表示的曲线是椭圆.( √ )(5)+=1(a≠b)表示焦点在 y 轴上的椭圆.( × )(6)+=1(a>b>0)与+=1(a>b>0)的焦距相等.( √ )2.小题热身(1)已知椭圆的方程为 2x2+3y2=m(m>0),则此椭圆的离心率为( B )A. B.C. D.(2)已知中心在原点的椭圆 C 的右焦点为 F(1,0),离心率等于,则椭圆 C 的方程是( D )A.+=1 B.+=1C.+=1 D.+=1(3)已知椭圆 C:+=1 的一个焦点为(2,0),则 C 的离心率为( C )A. B.C. D.(4)若方程+=1 表示椭圆,则 k 的取值范围是(3,4) ∪ (4,5) .(5)已知点 M(-2,0),N(2,0),点 P 是曲线 C:+y2=1(y≠0)上的动点,直线 PM 与 PN的斜率之积为-.解析:(1)由题意得椭圆的标准方程为+=1,所以 a2=,b2=,所以 c2=a2-b2=,e2==,e=.(2)设椭圆的标准方程为+=1(a>b>0).因为椭圆的一个焦点为 F(1,0),离心率 e=,所以解得故椭圆 C 的标准方程为+=1.(3) a2=4+2...