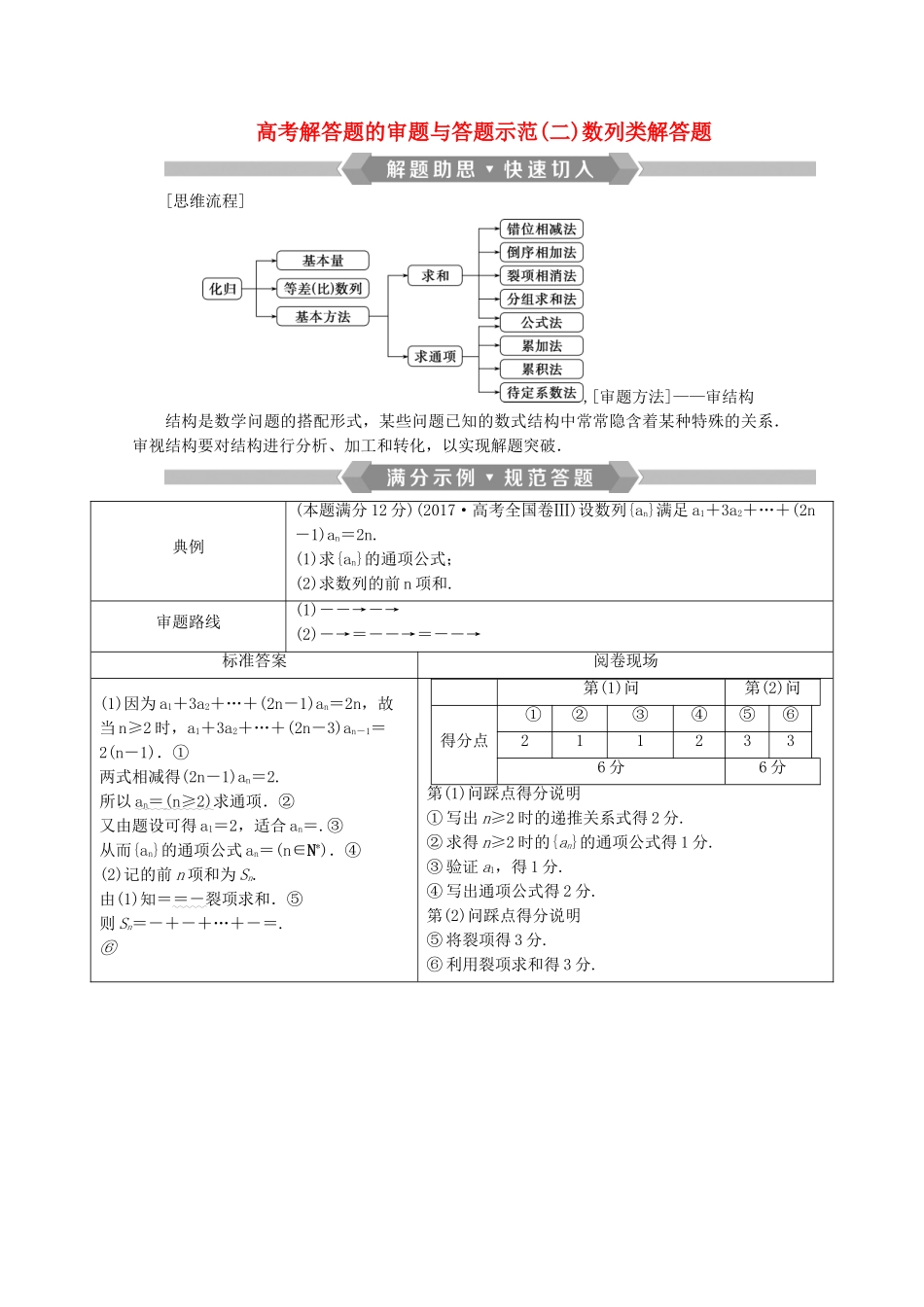
高考解答题的审题与答题示范(二)数列类解答题[思维流程],[审题方法]——审结构结构是数学问题的搭配形式,某些问题已知的数式结构中常常隐含着某种特殊的关系.审视结构要对结构进行分析、加工和转化,以实现解题突破.典例(本题满分 12 分)(2017·高考全国卷Ⅲ)设数列{an}满足 a1+3a2+…+(2n-1)an=2n.(1)求{an}的通项公式;(2)求数列的前 n 项和.审题路线(1)――→―→(2)―→=――→=-―→标准答案阅卷现场(1)因为 a1+3a2+…+(2n-1)an=2n,故当 n≥2 时,a1+3a2+…+(2n-3)an-1=2(n-1).①两式相减得(2n-1)an=2.所以 an= (n≥2) 求通项.②又由题设可得 a1=2,适合 an=.③从而{an}的通项公式 an=(n∈N*).④(2)记的前 n 项和为 Sn.由(1)知==-裂项求和.⑤则 Sn=-+-+…+-=.⑥第(1)问第(2)问得分点①②③④⑤⑥2112336 分6 分第(1)问踩点得分说明① 写出 n≥2 时的递推关系式得 2 分.② 求得 n≥2 时的{an}的通项公式得 1 分.③ 验证 a1,得 1 分.④ 写出通项公式得 2 分.第(2)问踩点得分说明⑤ 将裂项得 3 分.⑥ 利用裂项求和得 3 分.