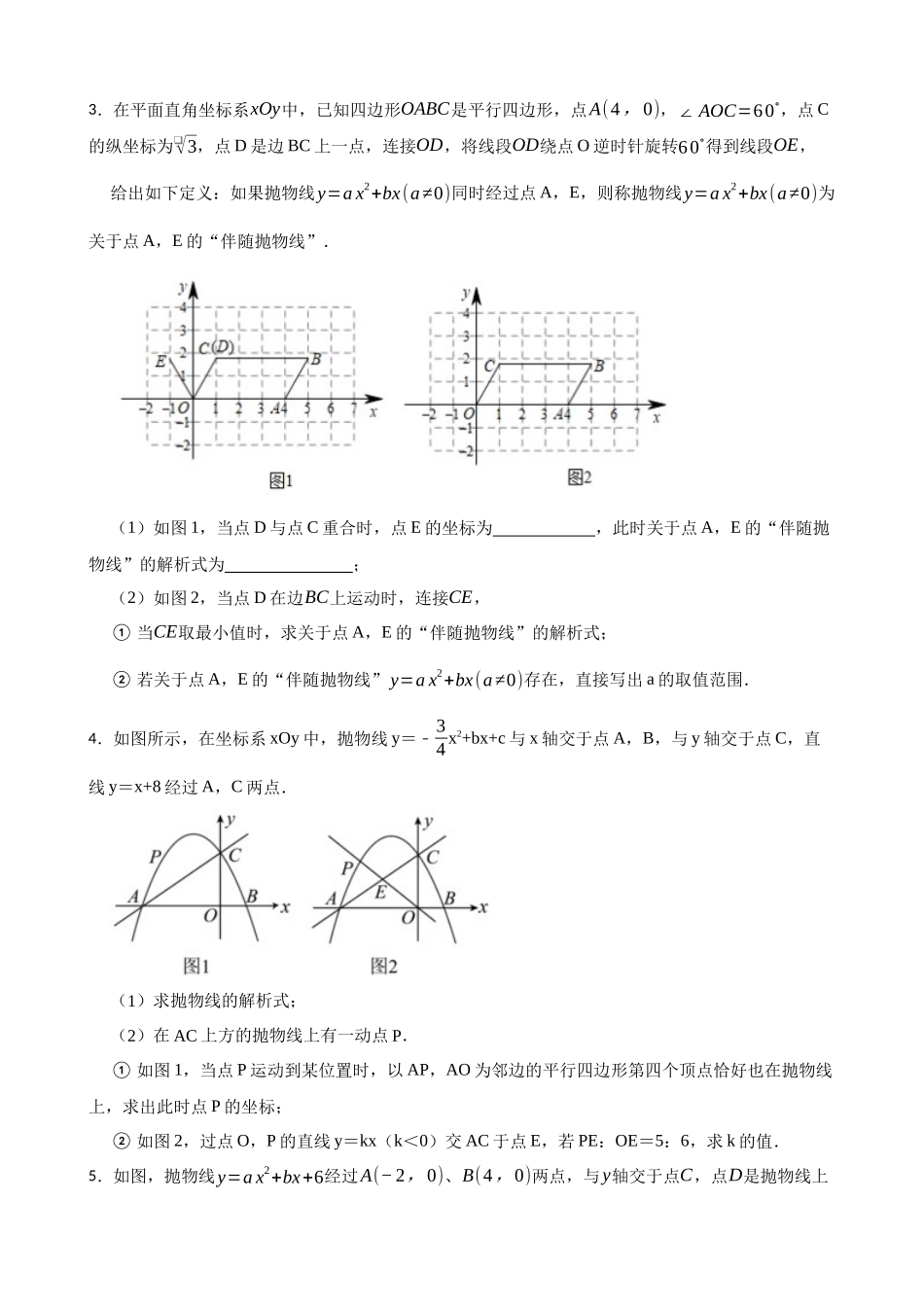
2026 年中考数学高频考点突破-二次函数与四边形一、综合题1.已知,如图抛物线y=a x2+3ax+c(a>0)与 y 轴交于点 C,与 x 轴交于 A,B 两点,点 A 在点 B左侧.点 B 的坐标为(1,0),OC=3OB.(1)求抛物线的解析式;(2)若点 D 是线段 AC 下方抛物线上的动点,求四边形 AOCD 面积的最大值;(3)若点 E 在 x 轴上,点 P 在抛物线上.是否存在以 A,C,E,P 为顶点且以 AC 为一边的平行四边形?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.2.如图,在平面直角坐标系中,直线y=2x+6与 x 轴交于点 A,与 y 轴交点 C,抛物线y=−2x2+bx+c过 A,C 两点,与 x 轴交于另一点 B.(1)求抛物线的解析式.(2)在直线AC上方的抛物线上有一动点 E,连接BE,与直线AC相交于点 F,当EF=12 BF时,求 E 点坐标.(3)在(2)的条件下,若点 E 位于对称轴左侧,点 M 是抛物线对称轴上一点,点 N 是抛物线上一点,当以 M,N,E,B 为顶点的四边形是菱形时,直接写出点 M 的坐标.3.在平面直角坐标系xOy中,已知四边形OABC是平行四边形,点A(4,0),∠ AOC=60∘,点 C的纵坐标为❑√3,点 D 是边 BC 上一点,连接OD,将线段OD绕点 O 逆时针旋转60∘得到线段OE,给出如下定义:如果抛物线y=a x2+bx(a≠0)同时经过点 A,E,则称抛物线y=a x2+bx(a≠0)为关于点 A,E 的“伴随抛物线”.(1)如图 1,当点 D 与点 C 重合时,点 E 的坐标为 ,此时关于点 A,E 的“伴随抛物线”的解析式为 ;(2)如图 2,当点 D 在边BC上运动时,连接CE,① 当CE取最小值时,求关于点 A,E 的“伴随抛物线”的解析式;② 若关于点 A,E 的“伴随抛物线”y=a x2+bx(a≠0)存在,直接写出 a 的取值范围.4.如图所示,在坐标系 xOy 中,抛物线 y=﹣34 x2+bx+c 与 x 轴交于点 A,B,与 y 轴交于点 C,直线 y=x+8 经过 A,C 两点.(1)求抛物线的解析式;(2)在 AC 上方的抛物线上有一动点 P.① 如图 1,当点 P 运动到某位置时,以 AP,AO 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点 P 的坐标;② 如图 2,过点 O,P 的直线 y=kx(k<0)交 AC 于点 E,若 PE:OE=5:6,求 k 的值.5.如图,抛物线y=a x2+bx+6经过A(−2,0)、B(4,0)两点,与y轴交于点C,点D是抛物线上一动点,设点D的横坐标为m(1