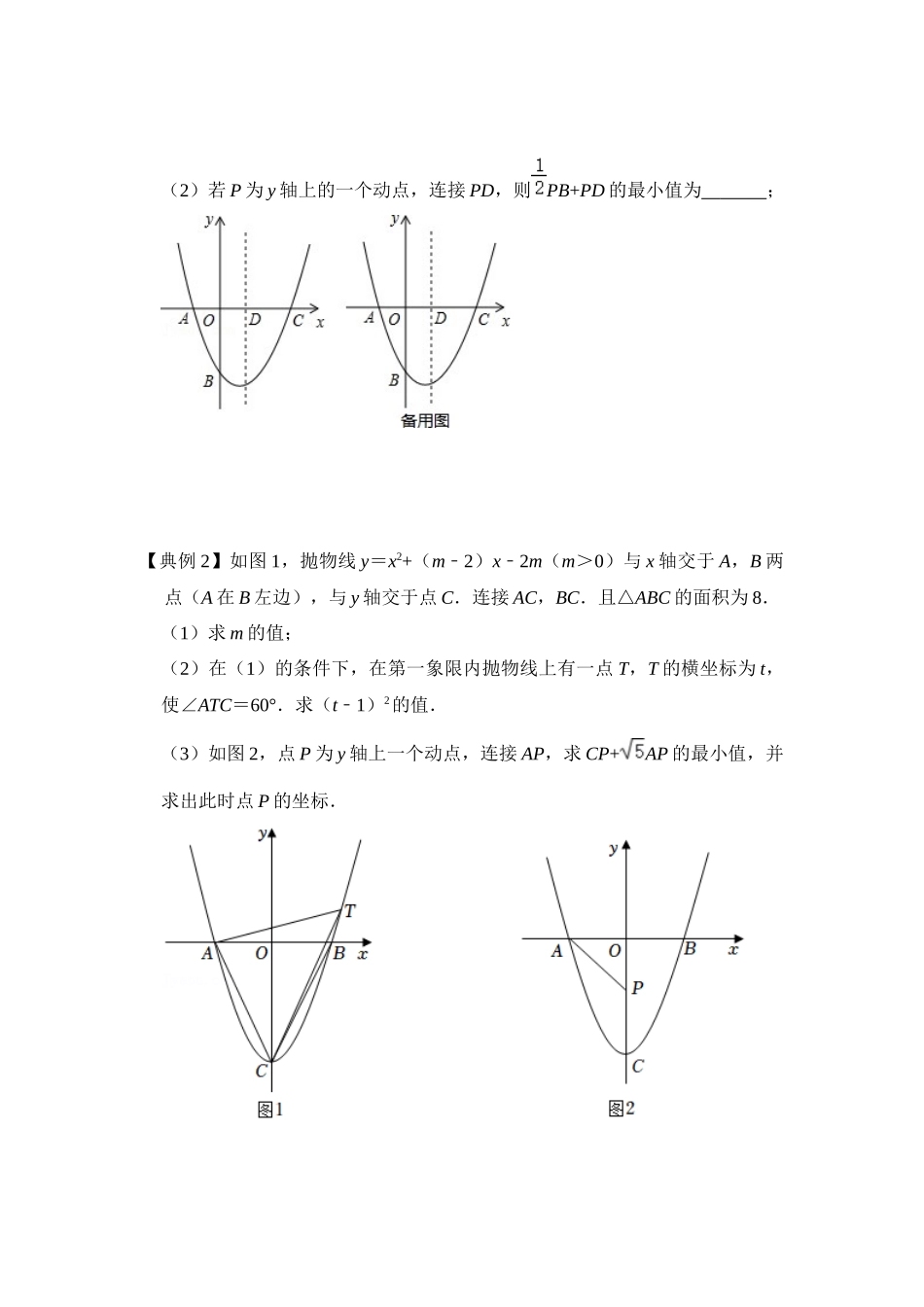
专题 09 二次函数与胡不归综合应用(知识解读)【专题说明】 “PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。此类问题的处理通常以动点 P 所在图像的不同来分类,一般分为 2 类研究。即点 P在直线上运动和点 P 在圆上运动。(1)其中点 P 在直线上运动的类型称之为“胡不归”问题;(2)点 P 在圆周上运动的类型称之为“阿氏圆”问题;前面几何模型中我们已经学习了“胡不归”解题方法。本章节继续学习二次函数与胡不归综合应用。【方法技巧】胡不归问题识别条件:动点 P 的运动轨迹是直线(或线段)方法:1、将所求线段和改为的形式()2、作,使 3、过点 B 作交 AC 于点 P4、的最小值转化为垂线段的长注意:当k>1时,【典例分析】【典例 1】如图,在平面直角坐标系中,二次函数 y=ax2+bx+c 的图象经过点A(﹣1,0),B(0,﹣),C(2,0),其对称轴与 x 轴交于点 D(1)求二次函数的表达式及其顶点坐标;(2)若 P 为 y 轴上的一个动点,连接 PD,则PB+PD 的最小值为 ;【典例 2】如图 1,抛物线 y=x2+(m2﹣ )x2﹣ m(m>0)与 x 轴交于 A,B 两点(A 在 B 左边),与 y 轴交于点 C.连接 AC,BC.且△ABC 的面积为 8.(1)求 m 的值;(2)在(1)的条件下,在第一象限内抛物线上有一点 T,T 的横坐标为 t,使∠ATC=60°.求(t1﹣ )2的值.(3)如图 2,点 P 为 y 轴上一个动点,连接 AP,求 CP+AP 的最小值,并求出此时点 P 的坐标.【变式 1】如图,已知抛物线 y=x24﹣ x+3 与 x 轴交于 A,B 两点(点 A 在点 B左侧),与 y 轴交于点 C.若点 Q 为线段 OC 上的动点,求 AQ+CQ 的最小值.所有【变式 2】如图,在平面直角坐标系中,直线 y=﹣x+4 的图象分别与 y 轴和 x轴交于点 A 和点 B.若定点 P 的坐标为(0,6),点 Q 是 y 轴上任意一点,则PQ+QB 的最小值为 .【 变 式 3 】 二 次 函 数 y = ax22﹣ x+c 的 图 象 与 x 轴 交 于 A 、 C 两 点 , 点C(3,0),与 y 轴交于点 B(0,﹣3).(1)a= ,c= ;(2)如图 1,P 是 x 轴上一动点,点 D(0,1)在 y 轴上,连接 PD,求PD+PC 的最小值;专题 09 二次函数与胡不归综合应用(知识解读)【专题说明】 “PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。此类问题的处理通常以动点 P 所在图...