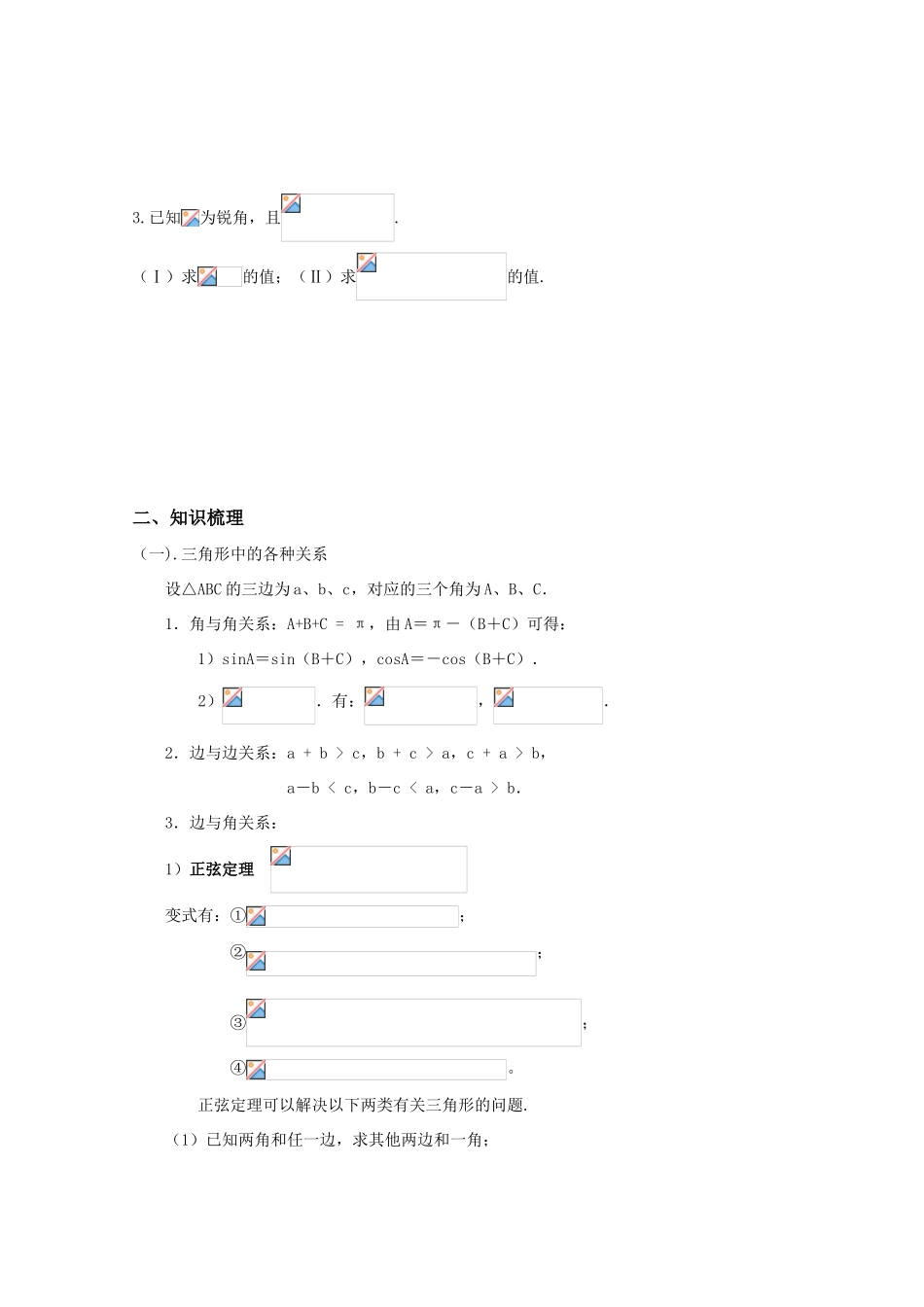
教案 12 解三角形(1)一、课前检测1.设函数(Ⅰ)求函数的最大值和最小正周期;(Ⅱ)设为的三个内角,若,,且为锐角,求的值.2.已知函数的图象如图所示.(Ⅰ)求的值;(Ⅱ)设,求函数的单调递增区间.3.已知为锐角,且.(Ⅰ)求的值;(Ⅱ)求的值.二、知识梳理(一).三角形中的各种关系设△ABC 的三边为 a、b、c,对应的三个角为 A、B、C.1.角与角关系:A+B+C = π,由 A=π-(B+C)可得:1)sinA=sin(B+C),cosA=-cos(B+C).2).有:,.2.边与边关系:a + b > c,b + c > a,c + a > b,a-b < c,b-c < a,c-a > b.3.边与角关系: 1)正弦定理 变式有:①;②;③;④。 正弦定理可以解决以下两类有关三角形的问题.(1)已知两角和任一边,求其他两边和一角;(2)已知两边和其中一边的对角,求另一边的对角.(从而进一步求出其他的边和角)2)余弦定理 c2 = a2+b2-2bccosC,b2 = a2+c2-2accosB,a2 = b2+c2-2bccosA.注:余弦定理是勾股定理的推广.变式有:cosA=;cosB=;cosC=.余弦定理,可以解决以下两类有关三角形的问题:(1)已知三边,求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角.3)射影定理: a=b·cosC+c·cosB,b=a·cosC+c·cosA,c=a·cosB+c·cosA.(二)面积公式(1)(分别表示 a、b、c 边上的高).(2).(3).(三)已知时三角形解的个数的判定: AbaCh其中 h=bsinA,A⑴ 为锐角时:① a
b 时,一解(锐角)。三、典型例题分析例 1 在△ABC 中,已知 a=,b=,B=45°,求角 A、C 及边 c.变式训练 1 (1)的内角 A、B、C 的对边分别为 a、b、c,若 a、b、c 成等比数列,且,则( )A. B. C. D.(2)在△ABC 中,由已知条件解三角形,其中有两解的是( )A. B. C. D.(3)在△ABC 中,已知,,则的值为( )A B C 或 D (4)若钝角三角形三边长为、、,则的取值范围是 .(5)在△ABC 中,= .(6)在中,,求.例 2 在中,已知,试判断的形状. 变式训练 2 在中,若,则必定是( ) A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形变式训练 3 在中,若,试判断的形状。 变式训练 4 在△ABC 中,若 sinA...