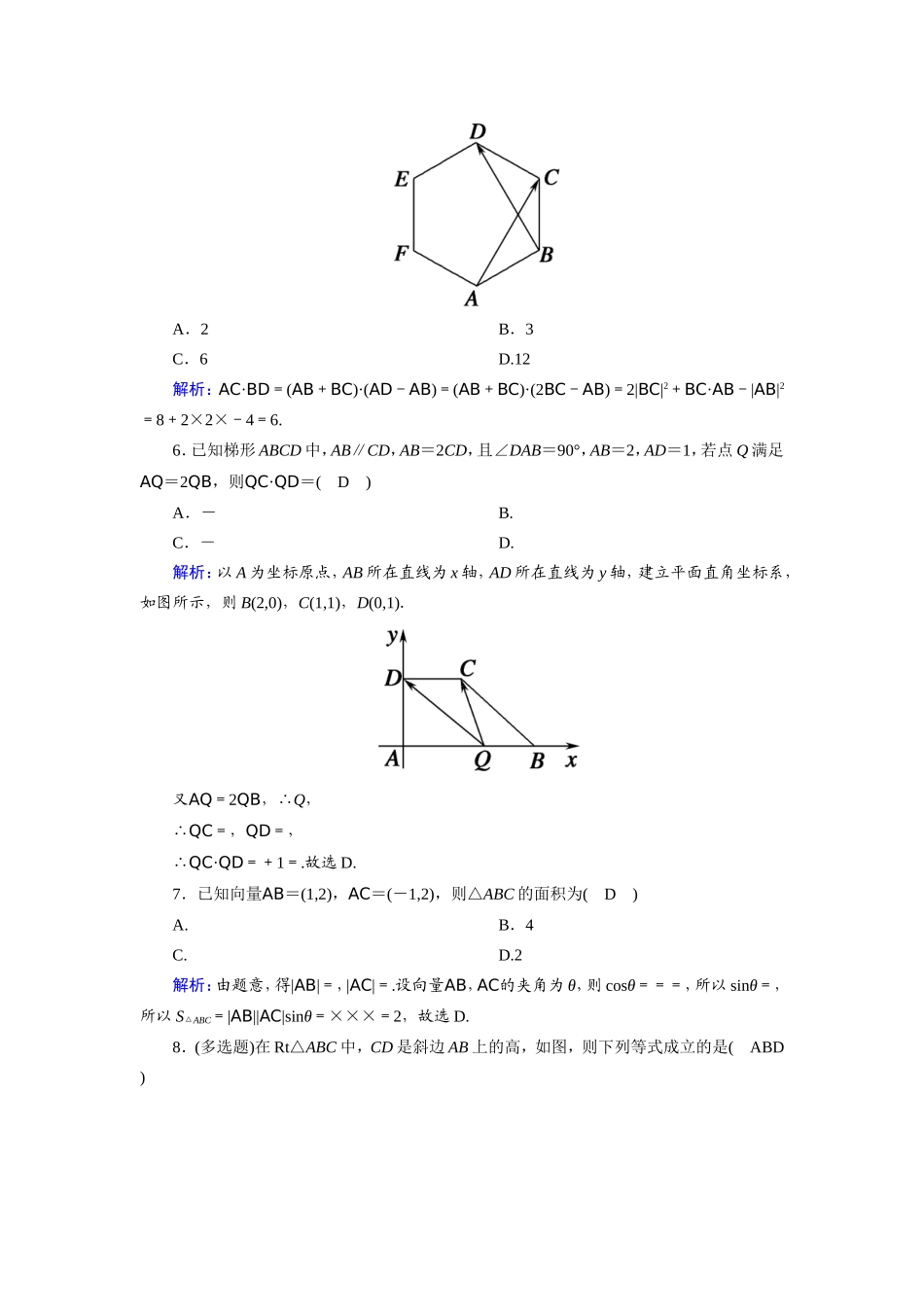
课时作业29平面向量的数量积一、选择题1.已知平面向量a,b的夹角为,且a·(a-b)=2,|a|=2,则|b|等于(D)A.B.2C.4D.2解析:因为a·(a-b)=2,所以a2-a·b=2,即|a|2-|a||b|cos〈a,b〉=2,所以4-2|b|×=2,解得|b|=2.2.已知向量a=(2,1),b=(2,x)不平行,且满足(a+2b)⊥(a-b),则x=(A)A.-B.C.1或-D.1或解析:因为(a+2b)⊥(a-b),所以(a+2b)·(a-b)=0,所以|a|2+a·b-2|b|2=0,因为向量a=(2,1),b=(2,x),所以5+4+x-2(4+x2)=0,解得x=1或x=-,因为向量a,b不平行,所以x≠1,所以x=-,故选A.3.已知向量a,b满足|a|=1,|b|=2,|a-b|=,则a与b的夹角为(A)A.B.C.πD.π解析:对|a-b|=两边平方得a2-2a·b+b2=3,即1-4cos〈a,b〉+4=3,解得cos〈a,b〉=,〈a,b〉=.故选A.4.已知向量a,b满足|a|=1,|b|=2,a·(a-2b)=0,则|a+b|=(A)A.B.C.2D.解析:由题意知,a·(a-2b)=a2-2a·b=1-2a·b=0,所以2a·b=1,所以|a+b|===.故选A.5.如图,正六边形ABCDEF的边长为2,则AC·BD=(C)A.2B.3C.6D.12解析:AC·BD=(AB+BC)·(AD-AB)=(AB+BC)·(2BC-AB)=2|BC|2+BC·AB-|AB|2=8+2×2×-4=6.6.已知梯形ABCD中,AB∥CD,AB=2CD,且∠DAB=90°,AB=2,AD=1,若点Q满足AQ=2QB,则QC·QD=(D)A.-B.C.-D.解析:以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立平面直角坐标系,如图所示,则B(2,0),C(1,1),D(0,1).又AQ=2QB,∴Q,∴QC=,QD=,∴QC·QD=+1=.故选D.7.已知向量AB=(1,2),AC=(-1,2),则△ABC的面积为(D)A.B.4C.D.2解析:由题意,得|AB|=,|AC|=.设向量AB,AC的夹角为θ,则cosθ===,所以sinθ=,所以S△ABC=|AB||AC|sinθ=×××=2,故选D.8.(多选题)在Rt△ABC中,CD是斜边AB上的高,如图,则下列等式成立的是(ABD)A.2=AC·ABB.2=BA·BCC.2=AC·CDD.2=解析:由AC·AB=|AC||AB|cosA=|AD||AB|,由射影定理可得|AC|2=AC·AB,即选项A正确,由BA·BC=|BA||BC|cosB=|BA||BD|,由射影定理可得|BC|2=BA·BC,即选项B正确,由AC·CD=|AC||CD|cos(π-∠ACD)<0,又|AB|2>0,即选项C错误,由图可知Rt△ACD∽Rt△ABC,所以|AC||BC|=|AB||CD|,由选项A,B可得|CD|2=,即选项D正确,故选ABD.二、填空题9.已知平面向量a,b满足|a|=|b|=1,a⊥(a-2b),则|a+b|=.解析: a⊥(a-2b),∴a·(a-2b)=0,解得2a·b=1,∴|a+b|==.10.已知向量a=(1,),b=(3,m)且b在a方向上的投影为-3,则向量a与b的夹角为.解析:因为b在a方向上的投影为-3,所以|b|cos〈a,b〉=-3,又|a|==2,所以a·b=|a||b|cos〈a,b〉=-6,又a·b=3+m,所以3+m=-6,解得m=-3,则b=(3,-3),所以|b|==6,所以cos〈a,b〉===-,因为0≤〈a,b〉≤π,所以a与b的夹角为.11.(多填题)如图,在菱形ABCD中,AB=2,∠BAD=60°,E,F分别是BC,CD的中点,若线段EF上有一点M满足AM=mAB+AD(m∈R),则m=,AM·BD=-.解析:解法1:设EM=λBD,在菱形ABCD中,E,F分别是BC,CD的中点,所以AM=AB+BE+EM=AB+AD+λBD=AB+AD+λ(AD-AB)=(1-λ)AB+(+λ)AD.又AM=mAB+AD,所以1-λ=m,+λ=,所以λ=,m=,所以AM=AB+AD,所以AM·BD=(AB+AD)·(AD-AB)=AD2-AB2+AB·AD.因为在菱形ABCD中,AB=2,∠BAD=60°,所以AM·BD=×4-×4+×2×2×cos60°=-.解法2:设AM与BD交于点P,则AP=AM=mAB+AD,因为B,P,D三点共线,所以m+=1,所以m=,所以AM=AB+AD,所以AM·BD=(AB+AD)·(AD-AB)=AD2-AB2+AB·AD.因为在菱形ABCD中,AB=2,∠BAD=60°,所以AM·BD=×4-×4+×2×2×cos60°=-.12.如图,在平面四边形ABCD中,AB⊥BC,AD⊥BD,∠BCD=60°,CB=CD=2,点M为BC边上一动点,则AM·DM的取值范围为.解析:如图,以点B为坐标原点,BC,BA所在的直线为x轴,y轴建立平面直角坐标系,则B(0,0),C(2,0),△BCD是等边三角形,则D(,3),BD=2,∠CBD=60°.又∠ABC=90°,则∠ABD=30°,则AB=4,A(0,4).又点M...