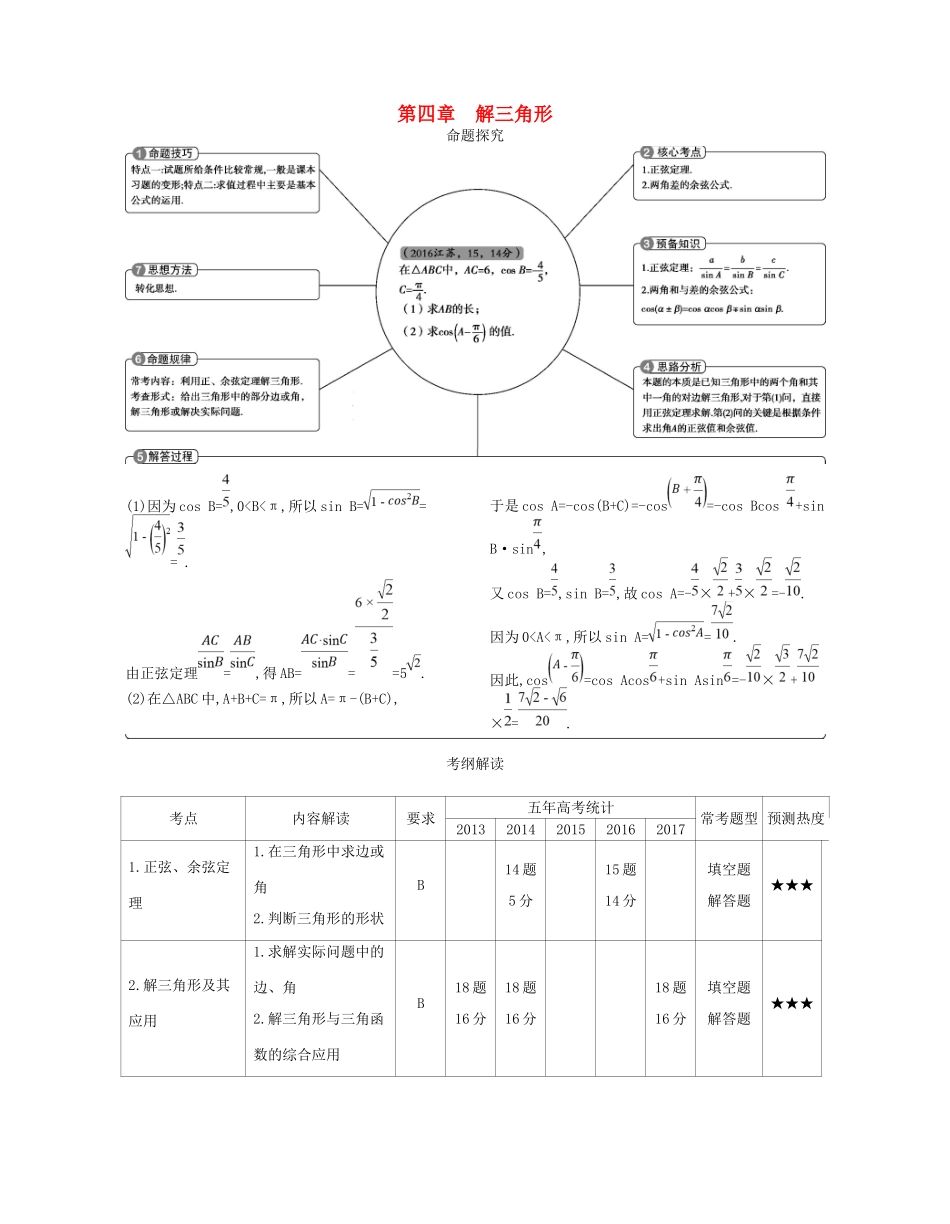
第四章解三角形命题探究(1)因为cosB=,00).则a=ksinA,b=ksinB,c=ksinC.代入+=中,有+=,变形可得sinAsinB=sinAcosB+cosAsinB=sin(A+B).在△ABC中,由A+B+C=π,得sin(A+B)=sin(π-C)=sinC,所以sinAsinB=sinC.(2)由已知,b2+c2-a2=bc,根据余弦定理的推论,有cosA==.所以sinA==.由(1),sinAsinB=sinAcosB+cosAsinB,所以sinB=cosB+sinB,故tanB==4.教师用书专用(11—18)11.(2017课标全国Ⅱ文,16,5分)△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=.答案60°12.(2017课标全国Ⅰ文改编,11,5分)△ABC的内角A,B,C的对边分别为a,b,c.已知sinB+sinA(sinC-cosC)=0,a=2,c=,则C=.答案13.(2017山东理改编,9,5分)在△ABC中,角A,B,C的对边分别为a,b,c.若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是.①a=2b;②b=2a;③A=2B;④B=2A.答案①14.(2014天津,12,5分)在△ABC中,内角A,B,C所对的边分别是a,b,c.已知b-c=a,2sinB=3sinC,则cosA的值为.答案-15.(2014课标Ⅰ,16,5分)已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)(sinA-sinB)=(c-b)sinC,则△ABC面积的最大值为.答案16.(2013浙江理,16,4分)在△ABC中,∠C=90°,M是BC的中点.若sin∠BAM=,则sin∠BAC=.答案17.(2014湖南,18,12分)如图,在平面四边形ABCD中,AD=1,CD=2,AC=.(1)求cos∠CAD的值;(2)若cos∠BAD=-,sin∠CBA=,求BC的长.解析(1)在△ADC中,由余弦定理,得cos∠CAD===.(2)设∠BAC=α,则α=∠BAD-∠CAD.因为cos∠CAD=,cos∠BAD=-,所以sin∠CAD===,sin∠BAD===.于是sinα=sin(∠BAD-∠CAD)=sin∠BADcos∠CAD-cos∠BADsin∠CAD=×-×=.在△ABC中,由正弦定理,得=,故BC===3.18.(2014辽宁,17,12分)在△ABC中,内角A,B,C的对边分别为a,b,c,且a>c.已知·=2,cosB=,b=3.求:(1)a和c的值;(2)cos(B-C)的值.解析(1)由·=2得c·acosB=2,又cosB=,所以ac=6.由余弦定理,得a2+c2=b2+2accosB.又b=3,所以a2+c2=9+2×2=13.解得a=2,c=3或a=3,c=2.因为a>c,所以a=3,c=2.(2)在△ABC中,sinB===,由正弦...