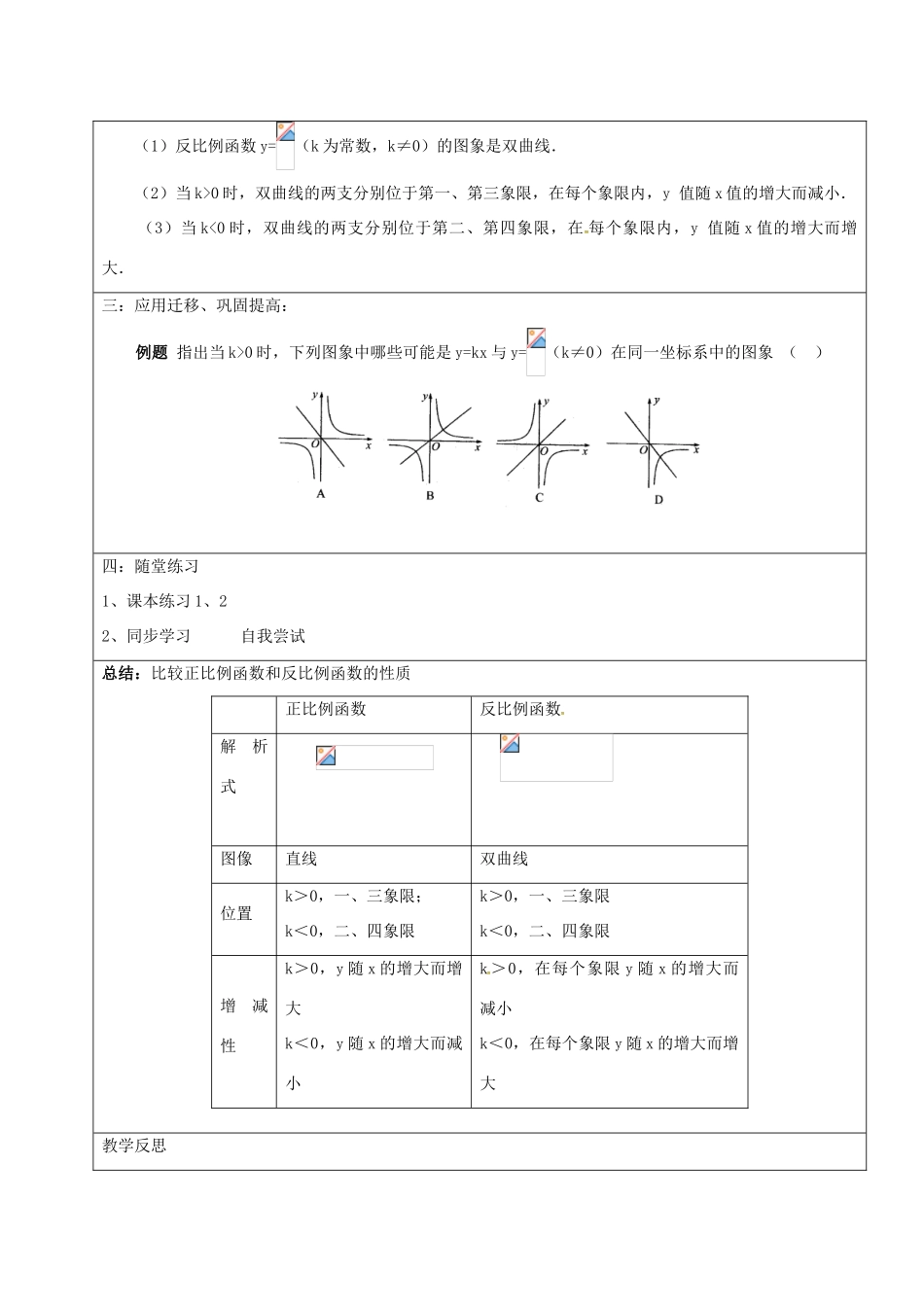
反比例函数的图象和性质课题26.1.2反比例函数的图象和性质(1)课型新授教学目标1、体会并了解反比例函数的图象的意义2、能描点画出反比例函数的图象3、通过反比例函数的图象的分析,探索并掌握反比例函数的图象的性质。4、结合正比例函数y=kx(k≠0)的图象和性质,来帮助学生观察、分析及归纳,通过对比,能使学生更好地理解和掌握所学的内容注意让学生体会数形结合的思想方法。5、以积极探索的思想,逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质。重点会作反比例函数的图象;探索并掌握反比例函数的主要性质。难点探索并掌握反比例函数的主要性质。教学过程与师生互动一:课堂引入提问:1.一次函数y=kx+b(k、b是常数,k≠0)的图象是什么?其性质有哪些?正比例函数y=kx(k≠0)呢?2.画函数图象的方法是什么?其一般步骤有哪些?应注意什么?方法与步骤——利用描点作图;列表:取自变量x的哪些值?——x是不为零的任何实数,所以不能取x的值的为零,但仍可以以零为基准,左右均匀,对称地取值。描点:依据什么(数据、方法)找点?连线:在各个象限内按照自变量从小到大的顺序用两条光滑的曲线把所描的点连接起来。二:探索新知:问题:我们已知道,一次函数y=kx+b(k≠0)的图象是一条直线,那么反比例函数y=(k为常数且k≠0)的图象是什么样呢?尝试用描点法来画出反比例函数的图象.探索活动【例2】画出反比例函数与的图象.解:1、列表(完成课本表格中的空白)2、描点,以表中各对应值为坐标,在直角坐标系中描出各点.3、连线,用平滑的曲线把所描的点依次连接起来.注意强调:(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值;(2)由于函数图象的特征还不清楚,所以要尽量多取一些数值,多描一些点,这样便于连线,使画出的图象更精确(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线;(4)由于x≠0,k≠0,所以y≠0,函数图象永远不会与x轴、y轴相交,只是无限靠近两坐标轴思考:反比例函数y=和y=-的图象有什么共同特征?它们之间有什么关系?做一做把y=和y=-的图象放到同一坐标系中,观察一下,看它们是否对称归纳反比例函数y=和y=-的图象的共同特征:(1)它们都由两条曲线组成.(2)随着的不断增大(或减小),曲线越来越接近坐标轴(x轴、y轴).(3)反比例函数的图象属于双曲线.此外,y=的图象和y=-的图象关于x轴对称,也关于y轴对称.做一做:课本练习在平面直角坐标系中画出反比例函数y=和y=-的图象.学生画图交流两个函数图象都用描点法画出?【思考】由y=和y=-的图象及y=和y=-的图象知道,(1)它们有什么共同特征和不同点?(2)每个函数的图象分别位于哪几个象限?(3)在每一个象限内,y随x的变化而如何变化?猜想反比例函数y=(k≠0)的图象在哪些象限由什么因素决定?在每一个象限内,y随x的变化情况如何?它可能与坐标轴相交吗?【归纳】反比例函数图象的特征及性质:(1)反比例函数y=(k为常数,k≠0)的图象是双曲线.(2)当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内,y值随x值的增大而减小.(3)当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内,y值随x值的增大而增大.三:应用迁移、巩固提高:例题指出当k>0时,下列图象中哪些可能是y=kx与y=(k≠0)在同一坐标系中的图象()四:随堂练习1、课本练习1、22、同步学习自我尝试总结:比较正比例函数和反比例函数的性质正比例函数反比例函数解析式图像直线双曲线位置k>0,一、三象限;k<0,二、四象限k>0,一、三象限k<0,二、四象限增减性k>0,y随x的增大而增大k<0,y随x的增大而减小k>0,在每个象限y随x的增大而减小k<0,在每个象限y随x的增大而增大教学反思课题26.1.2反比例函数的图象和性质(2)课型新授教学目标1.使学生进一步理解掌握反比例函数及图象与性质2.灵活运用函数图象和性质解决一些较综合的问题3.深刻领会函数解析式与函数图象之间的联系,体会数形结合及转化的...