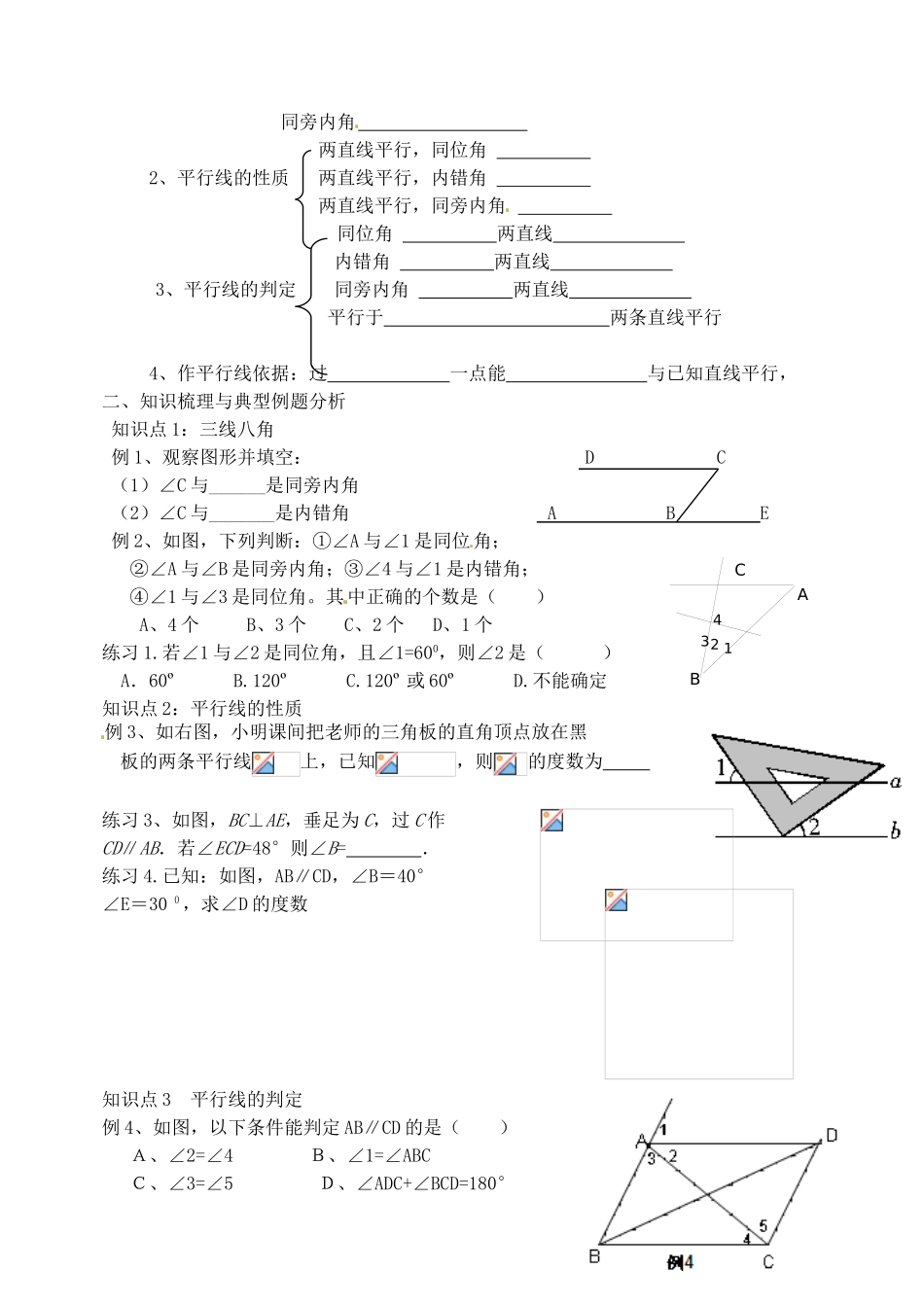
平行线姓名:班级复习目标:1、认识同位角,内错角,同旁内角。2、掌握过直线外一点能且只能作一条直线与已知直线平行,会用尺规作图,过直线外一点作这条直线的平行线。3、掌握平行线的性质及平行线的判定方法。教材分析图形的判定与图形的性质,是研究图形时必须要解决的问题。二者的不同之处在于平行线是条件还是结论。教科书通过学生已学过的平行线的画法中,有同位角相等画出的两直线就平行这一数学事实,得出“同位角相等,两直线平行”的判定方法。这一方法是判定两直线平行的基本方法,利用这一方法,通过对顶角和邻补角关系分别推出平行线的另外两种判定方法。教学目标1.知识与技能:(1)从“用三角尺和直尺画平行线的活动过程中发现”同位角相等,两直线平行;培养学生动手操作,主动探究及合作交流的能力。(2)会用平行线的判定方法判定两直线平行,初步学会用几何语言进行简单推理和表述。2.过程与方法:在探索图形的过程中,通过观察、操作、推理等手段,有条理地思考和表达自己地探索过程和结果,从而进一步加强学生分析,概括、表达能力。3.情感态度价值观:让学生在活动中体验探索、交流、成功与提升的喜悦,激发学生学习数学的兴趣,培养学生勇于实践,大胆猜想、推理的科学态度。复习重点:综合利用平行线的性质与判定解决简单的几何问题。复习难点:区别平行线的性质与判定,培养推理及语言表达能力。复习过程:一、知识网络体系(简单写)同位角(同侧,同旁)1、三线八角内错角同旁内角两直线平行,同位角2、平行线的性质两直线平行,内错角两直线平行,同旁内角同位角两直线内错角两直线3、平行线的判定同旁内角两直线平行于两条直线平行4、作平行线依据:过一点能与已知直线平行,二、知识梳理与典型例题分析知识点1:三线八角例1、观察图形并填空:DC(1)∠C与______是同旁内角(2)∠C与_______是内错角ABE例2、如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角。其中正确的个数是()A、4个B、3个C、2个D、1个练习1.若∠1与∠2是同位角,且∠1=600,则∠2是()A.60ºB.120ºC.120º或60ºD.不能确定知识点2:平行线的性质例3、如右图,小明课间把老师的三角板的直角顶点放在黑板的两条平行线上,已知,则的度数为练习3、如图,BC⊥AE,垂足为C,过C作CD∥AB.若∠ECD=48°则∠B=.练习4.已知:如图,AB∥CD,∠B=40°∠E=300,求∠D的度数知识点3平行线的判定例4、如图,以下条件能判定AB∥CD的是()A、∠2=∠4B、∠1=∠ABCC、∠3=∠5D、∠ADC+∠BCD=180°4321ABC练习5.如图,下列判断正确的是:()A、若∠1=∠2,则AD∥BCB、若∠1=∠2,则AB∥CDC、若∠A=∠3,则AD∥BCD、若∠3+∠ADC=180°,则AB∥CD练习6、如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=900那么直线AB、CD的位置关系如何?说明理由?知识点4综合利用平行线的性质与判定例5、已知:如图,AB∥CD,∠1=∠2.试判断BE与CF的位置关系,并说明理由。练习7、已知:如图AD⊥BC于D,EG⊥BC于G,∠E=∠3,试说明:AD是∠BAC的角平分线。三、小结:本节课所复习知识。四、课后作业1.下列语句中正确的是()(A)不相交的两条直线叫做平行线.(B)过一点有且只有一条直线与已知直线平行.(C)平面内两条直线被第三条直线所截,如果内错角相等,则同位角也相等(D)两条直线被第三条直线所截,同位角相等.2.已知,如图,AB∥CD,则∠α、∠β、∠γ之间的关系为()A.∠α+∠β+∠γ=360°B.∠α-∠β+∠γ=180°1ABDC23BGDCAE32154C.∠α+∠β-∠γ=180°D.∠α+∠β+∠γ=180°3.如图,由A到B的方向是()A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°4。如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论(1)AB//CD;(2)AD//BC;(3)∠B=∠D;(4)∠D=∠ACB。其中正确的有()A、1个B、2个C、3个D、4个5.已知:如图,AD∥BC,∠D=100°,AC平分∠BCD,求∠DAC的度数.ABCD12