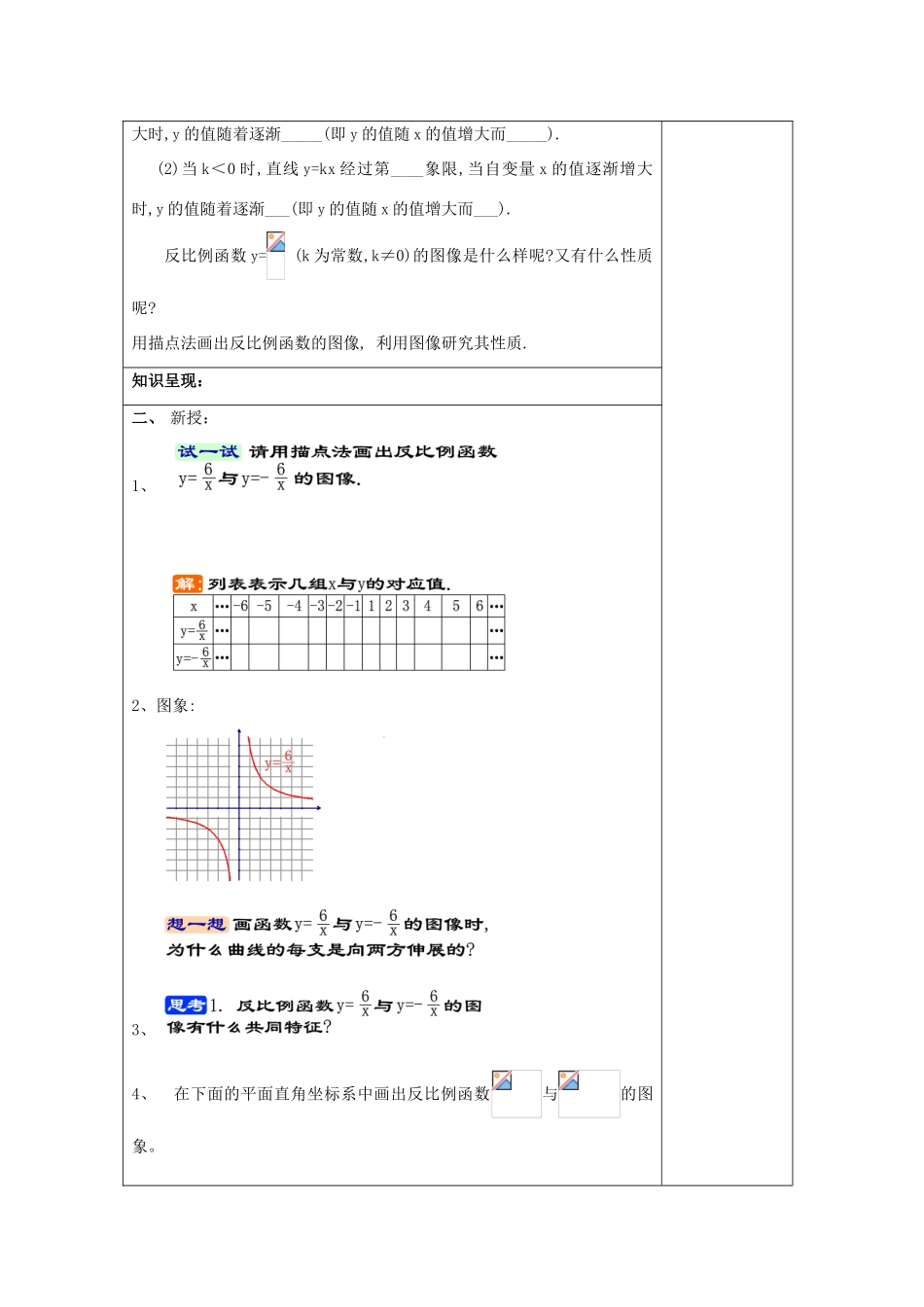
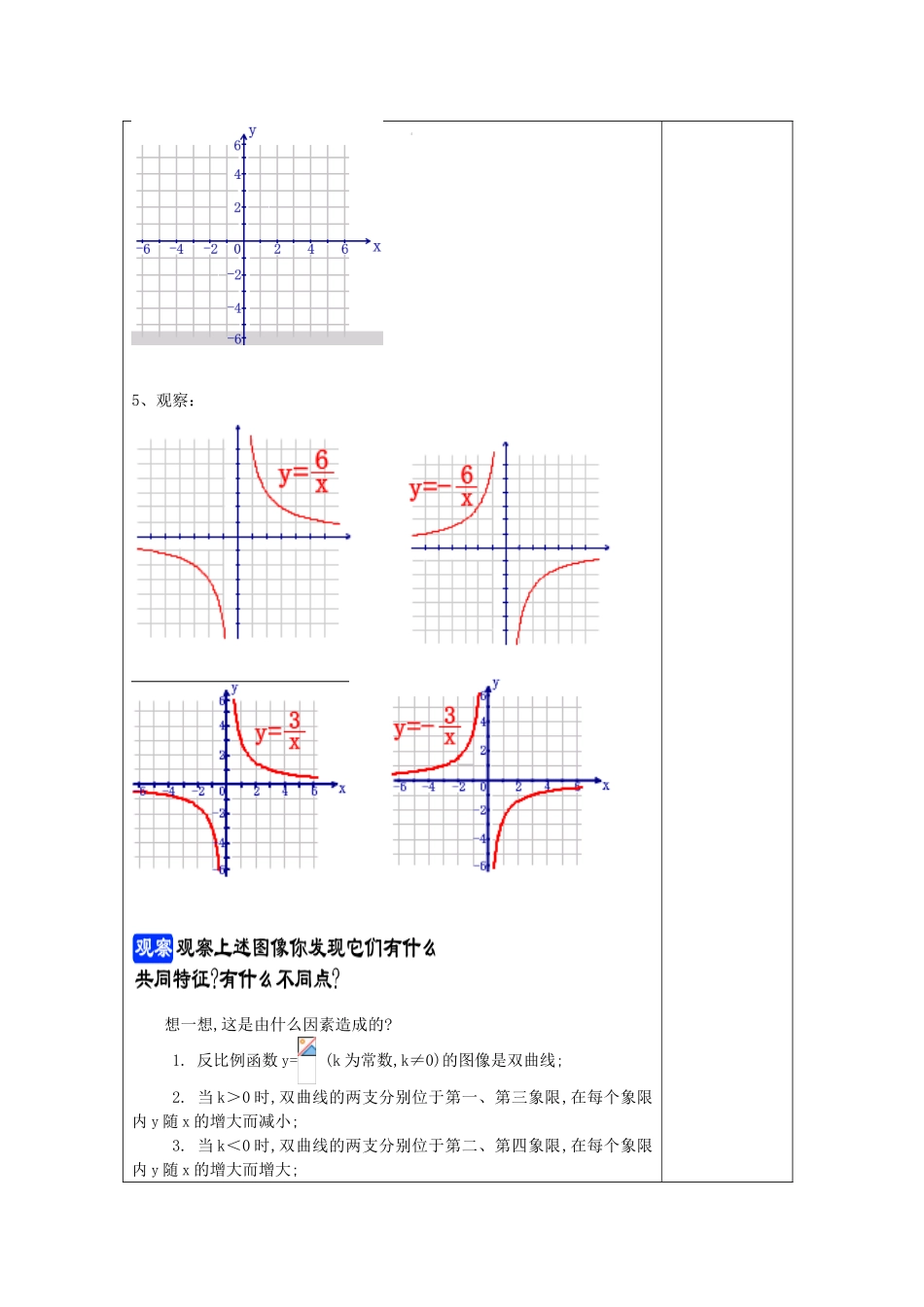
反比例函数的图像和性质课题18.3.2(1)反比例函数的图像和性质设计依据(注:只在开始新章节教学课必填)教材章节分析:学生学情分析:课型新授课教学目标1、通过画图像的操作实践,知道反比例函数的图像是双曲线,会描点法画反比例函数的图像。2、经历利用反比例函数图像直观探究的过程,体会数形结合的思想方法和研究函数的方法。3、在画图像的操作活动中,培养学生认真、细心、严谨的学习态度和学习习惯。重点掌握反比例函数图像的特征、性质,以及与正比例函数图像特征、性质的异同难点描点、光滑曲线画图、反比例函数的图像是双曲线,教学准备多媒体教学学生活动形式讨论,交流,总结,练习教学过程设计意图课题引入:一、复习:1.已知y与成反比例,且当x=4时,y=-3.求y与x的函数关系式.2.正比例函数y=kx(k是常数,k≠0)的图像是____________.(1)当k>0时,直线y=kx经过第_______象限,当自变量x的值逐渐增大时,y的值随着逐渐_____(即y的值随x的值增大而_____).(2)当k<0时,直线y=kx经过第____象限,当自变量x的值逐渐增大时,y的值随着逐渐___(即y的值随x的值增大而___).反比例函数y=(k为常数,k≠0)的图像是什么样呢?又有什么性质呢?用描点法画出反比例函数的图像,利用图像研究其性质.知识呈现:二、新授:1、2、图象:3、4、在下面的平面直角坐标系中画出反比例函数与的图象。5、观察:想一想,这是由什么因素造成的?1.反比例函数y=(k为常数,k≠0)的图像是双曲线;2.当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内y随x的增大而减小;3.当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内y随x的增大而增大;4.图像的两支都无限接近x轴和y轴,但不会与x轴和y轴相交.三、巩固练习:1、请指出下面的图像中哪一个是反比例函数的图像.2.在同一直角坐标平面内,分别画出下列函数的图像:请说一说上述图像中,自变量x逐渐增大时,y的值的变化情况.其中,图像位于第二、四象限的函数是___________;在其图像所在的每个象限内,y随x的值增大而减小的函数是_____.4.如果反比例函数y=的图像在第二、四象限,那么正比例函数y=kx的图像经过第_______象限.5.(1)当k____时,函数y=是反比例函数;(2)当k____时,反比例函数y=的图像的两个分支在第二、四象限内.(3)当k____时,反比例函数的图像在每个象限内y随x的增大而增大.课堂小结:四、本课小结:反比例函数的图像和性质1.反比例函数y=(k为常数,k≠0)的图像是双曲线;2.当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内y随x的增大而减小;3.当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内y随x的增大而增大;4.图像的两支都无限接近x轴和y轴,但不会与x轴和y轴相交.五、拓展练习:1.写出一个当x>0时,y随x增大而增大的反比例函数关系式____________.2.点P1(x1,y1)和点P2(x2,y2)都在反比例函数y=-的图象上,且x1<x2<0,则y1___y2(填“>”或“<”).3.思考反比例函数的图像是不是轴对称图形?是不是中心对称图形?如果是,请说出它的对称轴,对称中心.课外作业练习册习题18.3.2(1)预习要求18.3.2(2)反比例函数的图像和性质教学后记与反思1、课堂时间消耗:教师活动20分钟;学生活动20分钟)2、本课时实际教学效果自评(满分10分):分3、本课成功与不足及其改进措施: