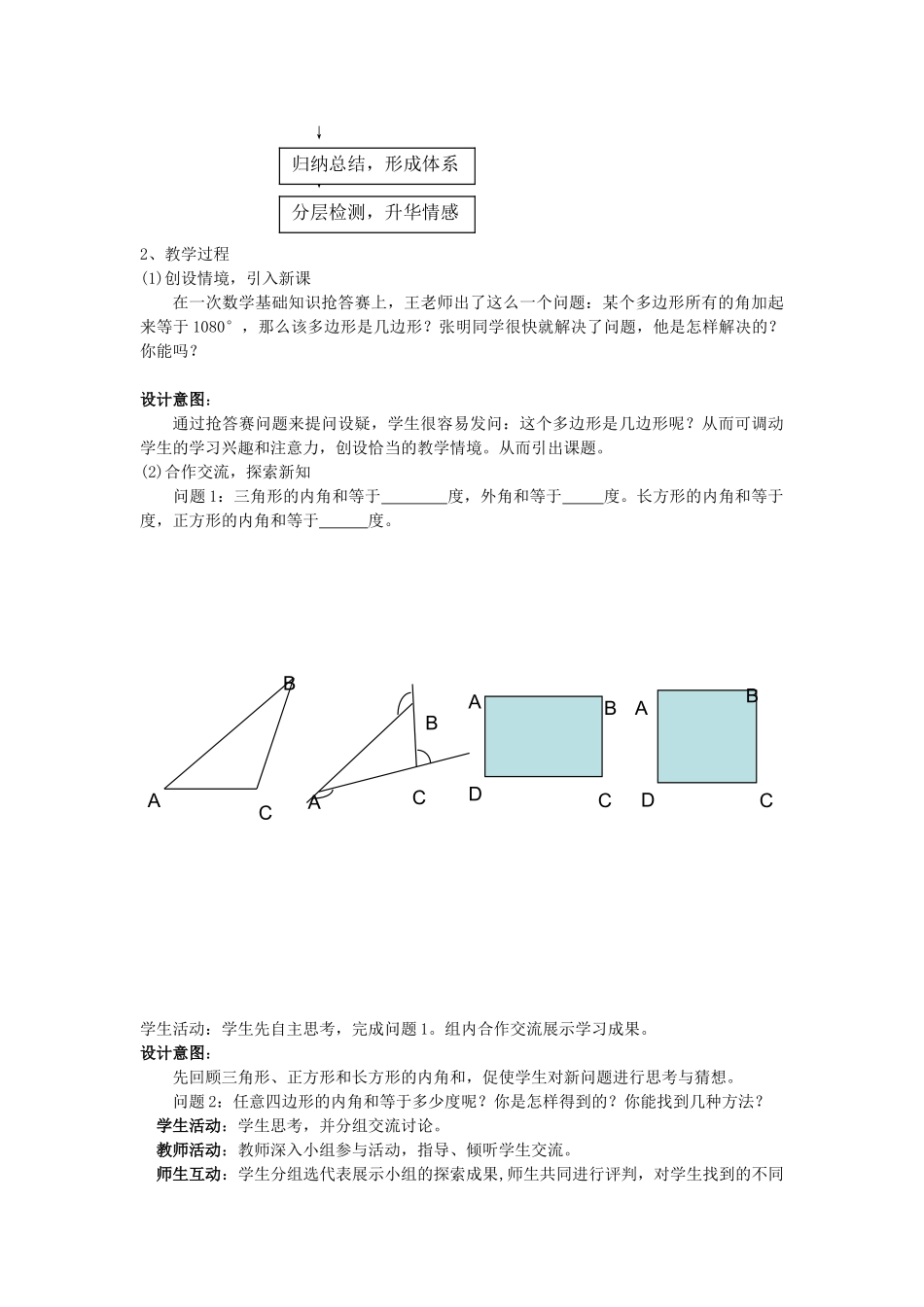
7.3.2《多边形的内角和》说课稿各位评委、老师,大家好!我说课的内容是人教版七年级下册第七章第三节第二课时《多边形的内角和》。我将从以下六个方面对本节课的教学设计进行说明。一、教材分析1、教材的地位和作用本节课作为第七章第三节,起着承上启下的作用。在内容上,从三角形的内角和到多边形的内角和,再将内角和公式应用于平面镶嵌,环环相扣,层层推进,这样易于激发学生的学习兴趣,很适合学生的认知特点。通过这节课的学习,可以培养学生探索与归纳能力,体会从简单到复杂,从特殊到一般和转化等重要的思想方法。2、教学重点和难点重点:多边形的内角和与外角和。难点:探索多边形内角和时,如何把多边形转化成三角形。二、教学目标分析1、知识与技能:掌握多边形的内角和与外角和,进一步了解转化的数学思想。2、数学思考:感受数学思考过程的条理性,发展推理能力和语言表达能力,并体会从特殊到一般的认识问题的方法。3、解决问题:让学生尝试通过不同方法探索多边形的内角和与外角和公式。并会应用它们进行有关计算。4、情感态度:让学生体验猜想得到证实的成就感,在解题中感受生活中数学的存在,体验数学充满探索和创造。三、教法和学法分析本着“解放学生的手,解放学生的大脑,解放学生的时间”的思想,我确定如下教法和学法:1、教学方法的设计整个学习的过程为了体现师生之间,生生之间的交流和互动,体现教师是教学活动的组织者、引导者、合作者,突出学生是学习的主体。所以,本节课我将采用探究式教学方法。2、学习方法在学习过程中,充分利用学生的好奇心设疑,解疑,组织活泼互动、有效的教学活动,鼓励学生积极参与,大胆猜想,使学生在自主探索和合作交流中理解和掌握本节课的内容。3、现代教育技术的应用在教学过程和学习过程中,我利用多媒体课件辅助教学,适时呈现问题情景,以丰富学生的感性认识,增强直观效果,提高课堂效率。四、教学过程分析1、本节教学将按以下六个流程展开↓↓↓创设情境,引入新课合作交流,探索新知自主探究,得出结论尝试练习,探索新知↓↓2、教学过程(1)创设情境,引入新课在一次数学基础知识抢答赛上,王老师出了这么一个问题:某个多边形所有的角加起来等于1080°,那么该多边形是几边形?张明同学很快就解决了问题,他是怎样解决的?你能吗?设计意图:通过抢答赛问题来提问设疑,学生很容易发问:这个多边形是几边形呢?从而可调动学生的学习兴趣和注意力,创设恰当的教学情境。从而引出课题。(2)合作交流,探索新知问题1:三角形的内角和等于度,外角和等于度。长方形的内角和等于度,正方形的内角和等于度。学生活动:学生先自主思考,完成问题1。组内合作交流展示学习成果。设计意图:先回顾三角形、正方形和长方形的内角和,促使学生对新问题进行思考与猜想。问题2:任意四边形的内角和等于多少度呢?你是怎样得到的?你能找到几种方法?学生活动:学生思考,并分组交流讨论。教师活动:教师深入小组参与活动,指导、倾听学生交流。师生互动:学生分组选代表展示小组的探索成果,师生共同进行评判,对学生找到的不同BACABCABCDABCD归纳总结,形成体系分层检测,升华情感方法要加以及时肯定。设计意图:从简单的四边形入手,让学生亲自操作寻求结论,易于引起学习兴趣,鼓励学生找到多种方法,学生可能找到以下几种方法:①“量”—即先测量四边形四个内角的度数,然后求四个内角的和;②“拼”—即把四边形的四个内角剪下来,拼在一起,得到一个周角③“分”—即通过添加辅助线的方法,把四边形分割成三角形,让学生体会多种分割形式教师在学生展示完后提问:在“量”、“拼”、“分”这几种方法中,哪种方法操作简单又相对准确?我们刚才找到了几种不同的辅助线的作法,它们的共同点是什么?有利于深入领会转化的本质——四边形转化为三角形,也让学生体验数学活动充满探索和解决问题方法的多样性。通过交流,让学生用自己的语言清楚地表达解决问题的过程,可以提高语言表达能力。(3)自主探究,得出结论问题1:用刚才认为简单的辅助线的方法,结合表格,算出五边形、六边形、七边形的内角和吗?学生活动:学生...