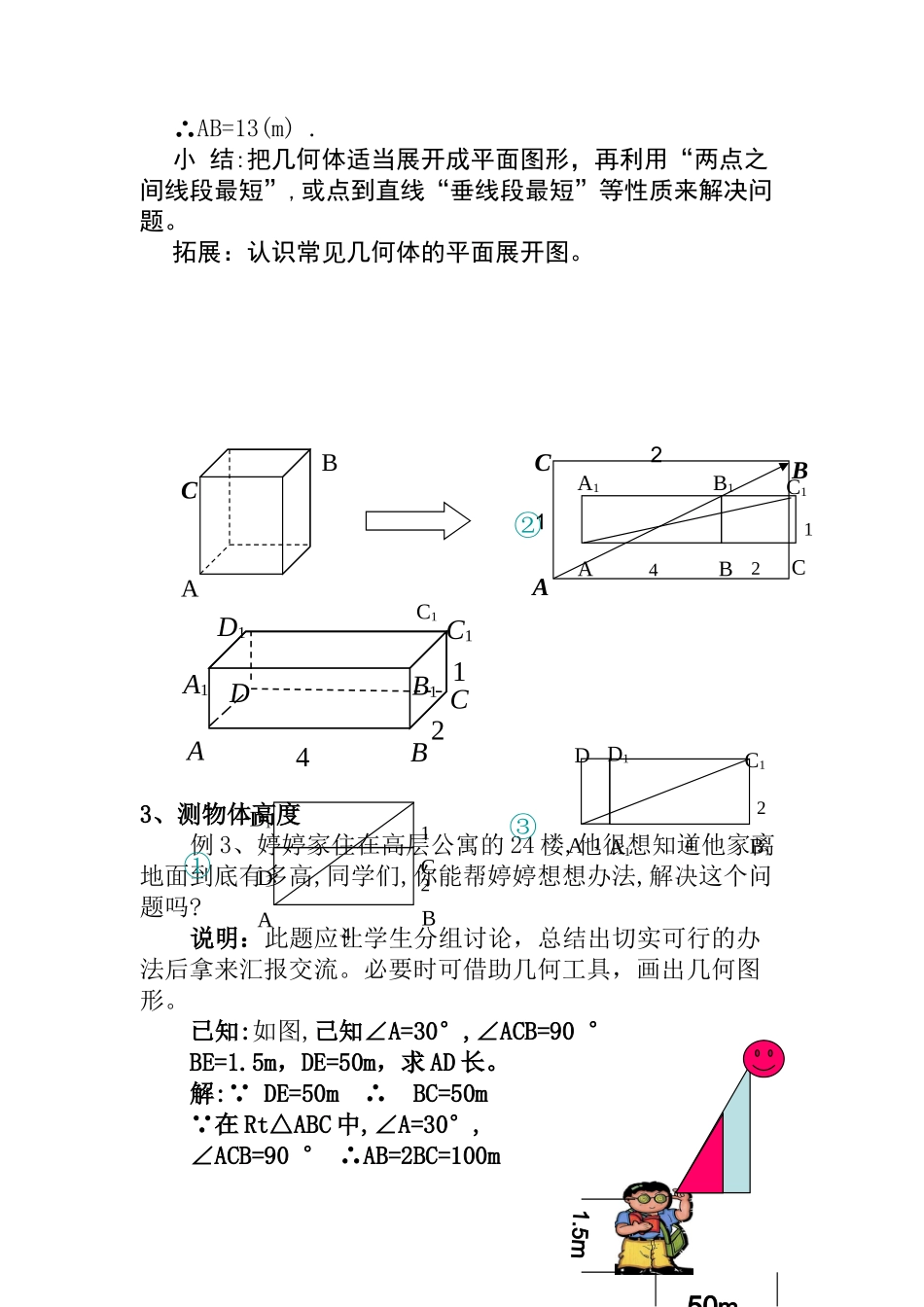
勾股定理的应用一、教学目标1、知识目标:(1)掌握勾股定理;(2)学会利用勾股定理进行计算、证明与作图;2、能力目标:(1)学会应用勾股定理解决实际问题,增强应用意识。(2)通过问题的解决,提高学生的运算能力和动手能力。(3)挖掘几何本质,探究几何规律。3、情感目标:(1)感受数学的巨大作用,培养学生勇于探索、勇于实践的精神。(2)培养善于合作与交流的团队精神,感受数学的美。二、教学重点、难点1、重点:勾股定理的熟练运用。2、难点:将实际问题转化为数学问题并用勾股定理解决。三、教学用具:三角板,微机四、教法以学生为主体的讨论探索法、情趣教学法五、学法1、动手实验法:引导学生寻找身边的实例,并想办法利用勾股定理去解决它。2、讨论验证法:通过观察图形,猜想结论,并加以证明。五、教学过程(一)新课背景知识(投影)1、回顾与思考:直角三角形的边、角之间分别存在着什么特殊的关系?引导学生回顾任意直角三角形边、角的关系,即Rt△ABC中,∠C=90°,a²+b²=c²,∠A+∠B=90°2、做一做:请学生举一个生活中的实例,并应用勾股定理解决它。(此项任务课前完成,教师及时整理,选取有代表性的问题拿到课上,由大家集体来探讨交流。)(二)实例展示(投影):说明:例题中均使用出题学生的小名,以示表扬,并促动其他学生,激发学习兴趣。1、电视机的大小问题例1、小菁妈妈买了一部29英寸(74厘米)的电视机.小菁量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?(1英寸=2.54厘米)(提示:电视机的大小是指荧屏对角线的长度)解:∵58²+46²=5480,74²=5476荧屏对角线大约为74厘米∴售货员没搞错2、几何体中最短路线问题例2、小良家有一底面周长为24m,高为6m的圆柱形油罐,一天他发现一只聪明的老鼠从距底面1m的A处爬行到对角B处吃食物,你知道小良为什么说那是只聪明的老鼠吗?(从爬行路线考虑)分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)解:AC=6–1=5,BC=24×1/2=12,由勾股定理得AB²=AC²+BC²=169,ABCBAC∴AB=13(m).小结:把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。拓展:认识常见几何体的平面展开图。3、测物体高度例3、婷婷家住在高层公寓的24楼,他很想知道他家离地面到底有多高,同学们,你能帮婷婷想想办法,解决这个问题吗?说明:此题应让学生分组讨论,总结出切实可行的办法后拿来汇报交流。必要时可借助几何工具,画出几何图形。已知:如图,己知∠A=30°,∠ACB=90°BE=1.5m,DE=50m,求AD长。解:∵DE=50m∴BC=50m∵在Rt△ABC中,∠A=30°,∠ACB=90°∴AB=2BC=100mABCABC21ABA1B1DCD1C1214AB1D1DA1C1③412ABDCD1①4211.5m50m②ABB1CA1C1412C1∴AC=√AB²-BC²=√10000-2500=50√3m∴AD=AC+CD=AC+BE=(50√3+1.5)m(三)学以致用:练1、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?练2、“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;小青观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅”请你帮助小青算出湖水的深度。(四)感悟与反思(让学生来小结本节课的内容):1、通过这节课的学习活动你有哪些收获?2、对这节课的学习,你还有什么想法吗?(五)试一试:布置作业P89T8、T9.30°50m1.5mABCDEA5B31DABC20.5XX+0.5