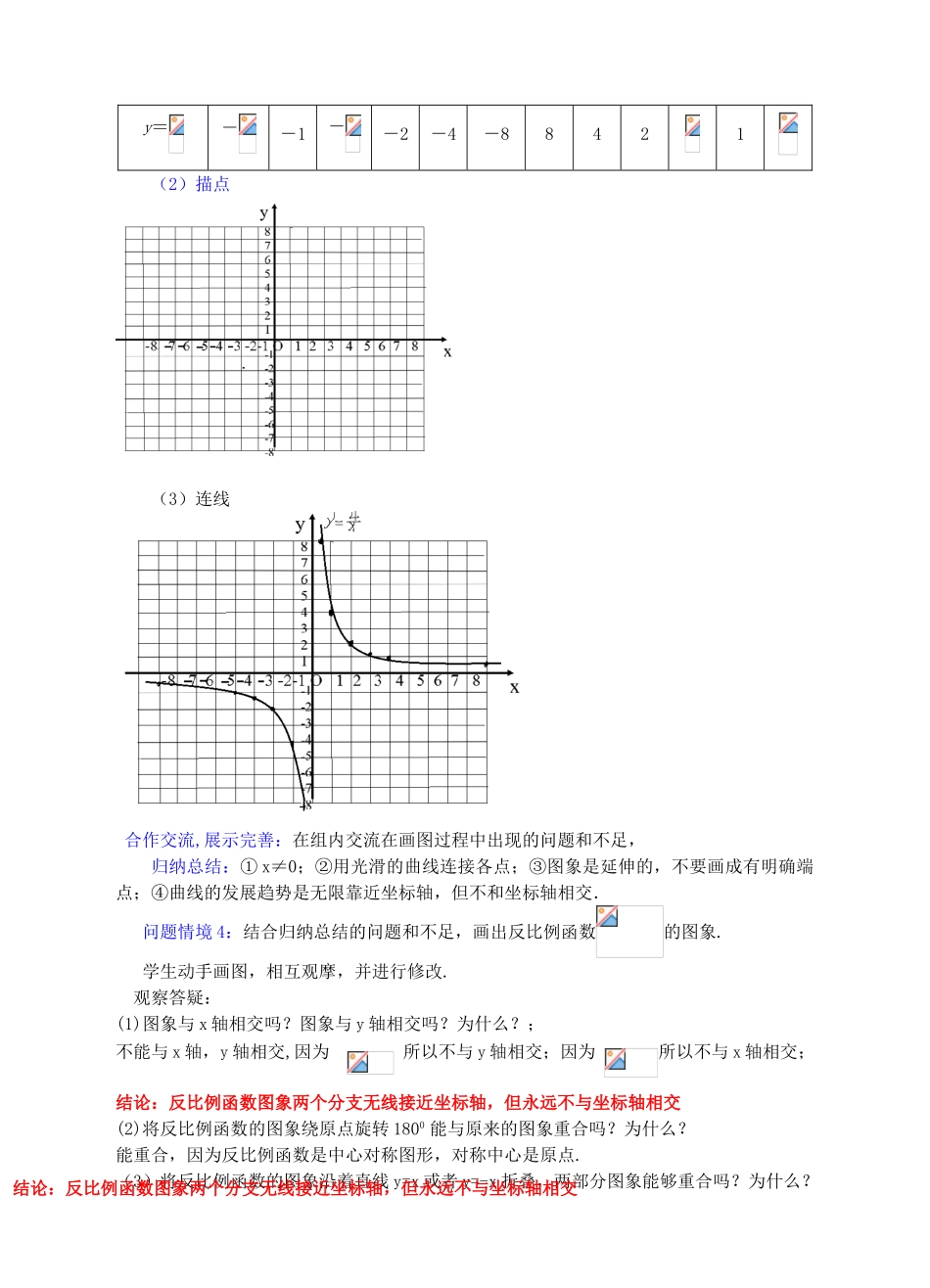
课题:6.2反比例函数图像和性质(1)教学目标:一、知识与技能目标:1.通过列表、描点、连线等步骤,作出反比例函数的图象;2.掌握反比例函数图象形的特点,掌握反比例函数图像与比例系数的关系;3.了解反比例函数的对称性.二、过程与方法目标:通过探索反比例函数的作图过程,了解反比例函数的作图特点;通过观察反比例函数的图象,总结反比例函数的性质.三、情感态度与价值观目标:在探索过程中培养学生的动手能力,在观察图象特点和总结性质的过程中,培养学生的审美感和总结归纳能力.重点:作反比例函数的图象;探索反比例函数图象的特点及性质.难点:探索反比例函数图象的特点及性质.教学流程:一、情景创设:复习情境1:正比例函数的图象是什么图形?正比例函数图象经过的象限与什么有关,图象都经过哪些象限?课堂展示:一次函数的图象是一条经过原点的直线;经过的象限与k有关:当k>0时,经过一、三象限;当k<0时,经过二、四象限.问题情境2:1.回顾反比例函数的定义?探究展示:一般的,把形如的函数叫做反比例函数.2画函数图象的步骤有哪些?在画反比例函数图象时应该注意哪些事项?画函数图象的步骤是:列表、描点、连线;在列表时要注意:反比例函数的定义中x的取值不能为0,列表时要避开0这个值;取值要取易于计算,易于描点的值..新课导入:猜想一下,反比例函数的图象是什么样子的?我们画一画看看.二、新知探究问题情境3:尝试画出反比例函数y=的图象自主探究:(1)列表x-8-4-3-2-1-12348y=--1--2-4-88421(2)描点(3)连线合作交流,展示完善:在组内交流在画图过程中出现的问题和不足,归纳总结:①x≠0;②用光滑的曲线连接各点;③图象是延伸的,不要画成有明确端点;④曲线的发展趋势是无限靠近坐标轴,但不和坐标轴相交.问题情境4:结合归纳总结的问题和不足,画出反比例函数的图象.学生动手画图,相互观摩,并进行修改.观察答疑:(1)图象与x轴相交吗?图象与y轴相交吗?为什么?;不能与x轴,y轴相交,因为所以不与y轴相交;因为所以不与x轴相交;结论:反比例函数图象两个分支无线接近坐标轴,但永远不与坐标轴相交(2)将反比例函数的图象绕原点旋转1800能与原来的图象重合吗?为什么?能重合,因为反比例函数是中心对称图形,对称中心是原点.(3)将反比例函数的图象沿着直线y=x或者y=-x折叠,两部分图象能够重合吗?为什么?结论:反比例函数图象两个分支无线接近坐标轴,但永远不与坐标轴相交能重合,因为反比例函数是轴对称图形,对称轴是y=x或y=-x.(4)函数与函数的图象有什么相同点和不同点?总结的图象在那两个象限,是由什么决定的?从形象和经过的经过一三,经过二四.由此我们得到:反比例函数的图象由k决定当k>0时,两支双曲线分别位于一、三象限内;当k<0时,两支双曲线分别位于二、四象限内象限三、典例探究:例题:做出反比例函数的图象,根据图象回答下列问题:(1)当x=2时,y的值;(2)当y=1时,x的值?(3)当y>2时,求x的范围.解:列表:x…-3-2-1123…y…-2-3-6632…描点,连线如图:由图可知:(1)y=3;(2)x=6;(3)0<x<3.四、尝试应用1.已知反比例函数的图象如图所示,则实数m的取值范围是()A.m>7B.m>0C.m<7D.m<02.下图给出了反比例函数和的图象,哪一个是的图象().3.已知反比例函数的图象经过点(1,-2),则这个函数的图象一定经过()A.(2,1)B.(2,-1)C.(2,4)D.(-1,-2)4.若,点A(b,a)在反比例函数的图象上,下列结论正确的是()A.B.C.D.5.已知反比例函数的图象在一三象限,那么一次函数的图象经过()A.一二三象限B.一二四象限C.一三四象限D.二三四象限达标测评1.反比例函数经过的象限()A.一三象限B.二四象限C.一二象限D.三四象限2.一个反比例函数经过二四象限,可能是下列那个函数()A.B.C.D.3.若函数与的图象交于第二、四象限,则m的取值范围是.4.反比例函数,当x=-2时,y=;当x<-2时;y的取值范围是;当x>-2时;y的取值范围是.5.已知反比例函数的图象在第二、四象限,求m值.六、拓展提升已知反比例函数y=(k≠0)和一次函数y=-x-4.若图象交于点(-...