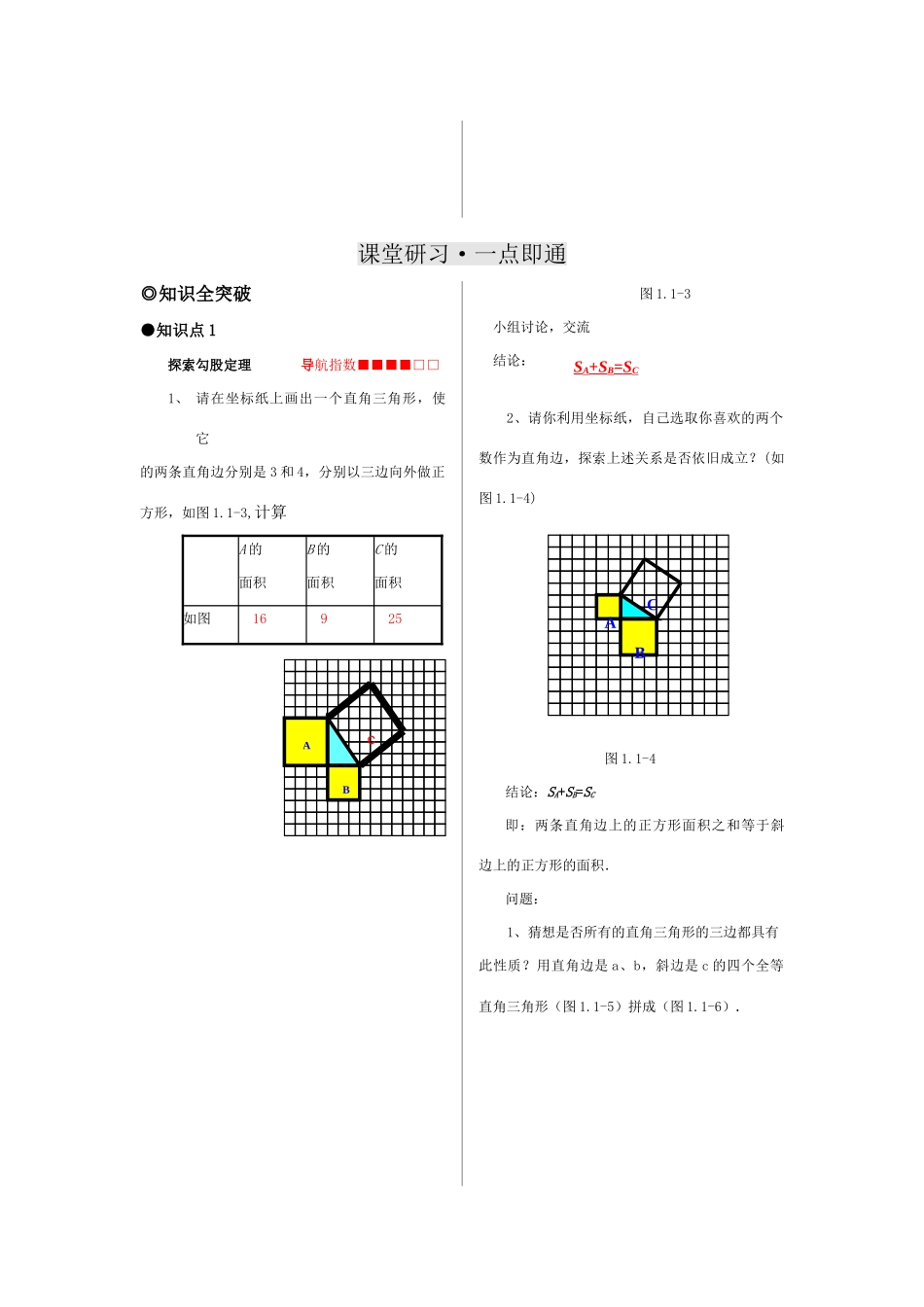
北师大版八年级数学(上册)教师用书第一章勾股定理1.1探索勾股定理课前预习·教学有方◎点击关键词勾股定理平方证明计算应用◎目标导航船1.通过拼图活动和勾股定理的文化背景了解,让学生发现勾股定理.2.能利用材料,通过剪、拼图验证勾股定理.3.能运用勾股定理根据直角三角形的两条边求第三条边,并能解决简单的生活、生产实践中的问题.3.重点:勾股定理的证明及应用。4.难点:学生数学语言的运用。◎创意开场白勾股定理是在前面学习了直角三角形一些性质的基础上学习的,它是几何的重要定理之一,它揭示了直角三角形三边的数量关系,它将形与数密切联系起来,在数学的发展中起着非常重要的作用,在现实世界中也有着广泛的应用.学生通过对勾股定理的学习,对直角三角形有进一步的认识和理解,为今后学习解直角三角形打下基础。一、欣赏图片引人2002年国际数学家大会把“赵爽弦图”确定为本届大会的会徽。你见过这个图案吗?你听说过勾股定理吗?引入新课§18.1勾股定理二、了解历史引人商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:"…故折矩,勾广三,股修四,经隅五。"什么是"勾、股"呢?在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成"勾三股四弦五"。由于勾股定理的内容最早见于商高的话中,所以人们就把这个定理叫作"商高定理"。三、从一个美丽的故事引人世界的许多科学家正在试探着寻找“外星人”,人们为了取得与外星人的联系,想了很多方法。早在1820年,德国著名数学家高斯曾提出,可在西伯利亚的森林里伐出一片直角三角形的空地,然后在这片空地里种上麦子,以三角形的三条边为边种上三片正方形的松树林,如果有外星人路过地球附近,看到这个巨大的数学图形,便会知道:这个星球上有智慧生命。我国数学家华罗庚也曾提出:若要沟通两个不同星球的信息交往,最好利用太空飞船带上这个图形,并发射到太空中去。四、从一个著名问题引人《九章算术》有一勾股定理名题:“今有池方一丈,葭(jiā)生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.”本题的意思是:(如图1)有一水池一丈见方,池中生有一棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐。问水有多深,该植物有多长?教师通过将实际问题转化成直角三角形的三边关系问题,从而出示课题——勾股定理。◎温故而知新【温故】1、三角形按照角的大小可以分为:锐角三角形、直角三角形、和钝角三角形。2、三角形的三边关系:任意两边之和大于第三边。【知新】勾股定理:1.直角三角形两直角边的平方和等于斜边的平方.2.几何语言表述:如图1.1-1,在RtΔABC中,C=90°。则:BC2+AC2=AB2若BC=a,AC=b,AB=c,则上面的定理可以表示为:图1.1-1乐学好思1到目前为止,学过的直角△ABC的主要性质是:(如图1.1-2)∠C=90°,(用几何语言表示)⑴两锐角之间的关系:;⑵若D为斜边中点,则斜边中线等于斜边的一半;⑶若∠B=30°,则∠B的对边和斜边:;⑷三边之间的关系:.图1.1-2我的疑问:5尺1尺x尺(x-1)尺DACABD图1ABCD课堂研习·一点即通◎知识全突破●知识点1探索勾股定理导航指数■■■■□□1、请在坐标纸上画出一个直角三角形,使它的两条直角边分别是3和4,分别以三边向外做正方形,如图1.1-3,计算A的面积B的面积C的面积如图16925图1.1-3小组讨论,交流结论:2、请你利用坐标纸,自己选取你喜欢的两个数作为直角边,探索上述关系是否依旧成立?(如图1.1-4)图1.1-4结论:SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.问题:1、猜想是否所有的直角三角形的三边都具有此性质?用直角边是a、b,斜边是c的四个全等直角三角形(图1.1-5)拼成(图1.1-6).ABCSA+SB=SCABC观察图形并思考、填空:大正方形的面积可表示为:(a+b)2这个大正方形的面积还可以怎么表示?;于是可列...