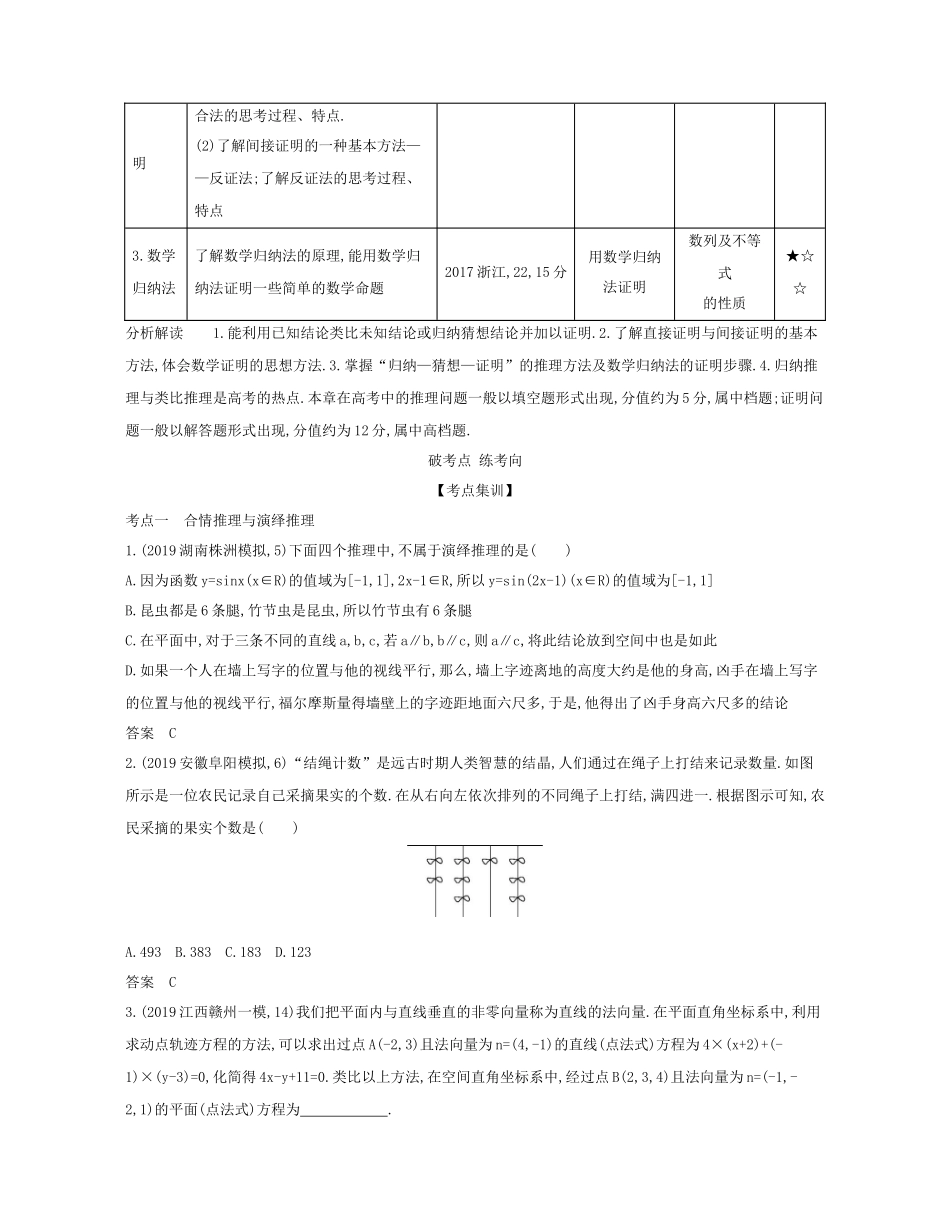
专题十三推理与证明探考情悟真题【真题探秘】【考情探究】考点内容解读5年考情预测热度考题示例考向关联考点1.合情推理与演绎推理(1)了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用.(2)了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单推理.(3)了解合情推理和演绎推理之间的联系和差异2019课标Ⅰ,4,5分运用黄金分割估计身高不等式性质★☆☆2017课标Ⅱ,7,5分根据给出的说法进行推理2016课标Ⅱ,15,5分根据给出的说法进行推理2.直接证明与间接证(1)了解直接证明的两种基本方法——分析法和综合法;了解分析法和综2018江苏,19,16分直接证明利用导数研究函数的性质★☆☆明合法的思考过程、特点.(2)了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点3.数学归纳法了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题2017浙江,22,15分用数学归纳法证明数列及不等式的性质★☆☆分析解读1.能利用已知结论类比未知结论或归纳猜想结论并加以证明.2.了解直接证明与间接证明的基本方法,体会数学证明的思想方法.3.掌握“归纳—猜想—证明”的推理方法及数学归纳法的证明步骤.4.归纳推理与类比推理是高考的热点.本章在高考中的推理问题一般以填空题形式出现,分值约为5分,属中档题;证明问题一般以解答题形式出现,分值约为12分,属中高档题.破考点练考向【考点集训】考点一合情推理与演绎推理1.(2019湖南株洲模拟,5)下面四个推理中,不属于演绎推理的是()A.因为函数y=sinx(x∈R)的值域为[-1,1],2x-1∈R,所以y=sin(2x-1)(x∈R)的值域为[-1,1]B.昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿C.在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c,则a∥c,将此结论放到空间中也是如此D.如果一个人在墙上写字的位置与他的视线平行,那么,墙上字迹离地的高度大约是他的身高,凶手在墙上写字的位置与他的视线平行,福尔摩斯量得墙壁上的字迹距地面六尺多,于是,他得出了凶手身高六尺多的结论答案C2.(2019安徽阜阳模拟,6)“结绳计数”是远古时期人类智慧的结晶,人们通过在绳子上打结来记录数量.如图所示是一位农民记录自己采摘果实的个数.在从右向左依次排列的不同绳子上打结,满四进一.根据图示可知,农民采摘的果实个数是()A.493B.383C.183D.123答案C3.(2019江西赣州一模,14)我们把平面内与直线垂直的非零向量称为直线的法向量.在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A(-2,3)且法向量为n=(4,-1)的直线(点法式)方程为4×(x+2)+(-1)×(y-3)=0,化简得4x-y+11=0.类比以上方法,在空间直角坐标系中,经过点B(2,3,4)且法向量为n=(-1,-2,1)的平面(点法式)方程为.答案x+2y-z-4=0考点二直接证明与间接证明1.(2019湖南张家界模拟,5)用反证法证明命题“已知a、b、c为非零实数,且a+b+c>0,ab+bc+ca>0,求证a、b、c中至少有两个为正数”时,要做的假设是()A.a、b、c中至少有两个为负数B.a、b、c中至多有一个为负数C.a、b、c中至多有两个为正数D.a、b、c中至多有两个为负数答案A2.(2018湖北普通高中联考,7)分析法又叫执果索因法,若使用分析法证明:设a0B.c-a>0C.(c-b)(c-a)>0D.(c-b)(c-a)<0答案C考点三数学归纳法(2020届吉林延边二中高三开学考试,4)用数学归纳法证明“1+2+3+…+n3=n6+n32,n∈N*”,则当n=k+1(k∈N*)时,左端应在n=k的基础上加上()A.(k3+1)+(k3+2)+…+(k+1)3B.(k3+1)+(k3+2)+…+(k3+k+1)C.(k+1)3D.(k+1)6+(k+1)32答案A炼技法提能力【方法集训】方法归纳推理与类比推理的应用1.(2019湖南邵阳二模,9)在平面几何里有射影定理:设三角形ABC的两边AB⊥AC,D是A点在BC上的射影,则AB=BD·BC.拓展到空间,在四面体ABCD中,AD⊥面ABC,点O是A在面BCD内的射影,且O在△BCD内,类比平面三角形射影定理,得出正确的结论是()A.S△ABC2=S△BCO·S△BCDB.S△ABD2=S△BOD·S△BOCC.S△ADC2=S△DOC·S△BOCD.S△BDC2=S△ABD·S△ABC答案A2.(2019安徽六安高三下学期开学考试,16)观察下列等式:13+23=1;73+83+103+113=12;163+173+193+203+223+233=39;……则当n