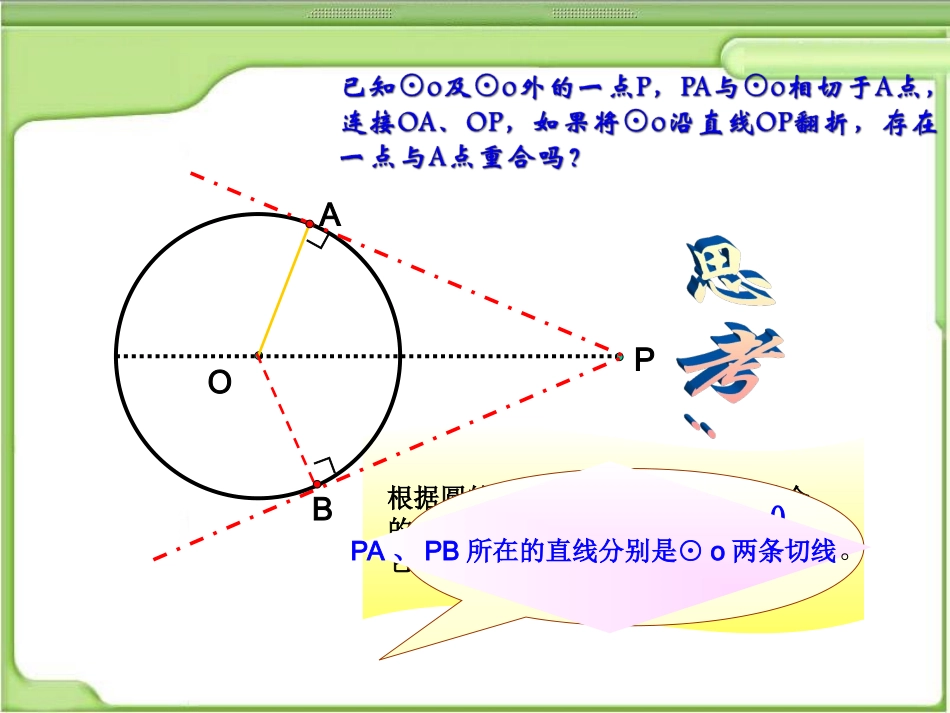
24.2.2切线长定理根据圆的轴对称性,存在与A点重合的一点B,且落在圆,连接OB,则它也是⊙o的一条半径。OPAB你能发现OA与PA,OB与PB之间的关系吗?PA、PB所在的直线分别是⊙o两条切线。∟∟在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长·OPAB切线与切线长是一回事吗?··它们有什么区别与联系呢?切线和切线长是两个不同的概念:1、切线是一条与圆相切的直线,不能度量;2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。OPAB比一比比一比OABP思考:已知⊙O切线PA、PB,A、B为切点,把圆沿着直线OP对折,你能发现什么?12折一折折一折请证明你所发现的结论。APOBPA=PB∠OPA=OPB∠证明: PA,PB与⊙O相切,点A,B是切点∴OA⊥PA,OB⊥PB即∠OAP=OBP=90°∠ OA=OB,OP=OP∴Rt△AOP≌Rt△BOP(HL)∴PA=PBOPA=OPB∠∠试用文字语言叙述你所发现的结论证一证证一证PA、PB分别切⊙O于A、BPA=PB∠OPA=OPB∠从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。几何语言:反思:切线长定理为证明线段相等、角相等提供新的方法OPAB切线长定理切线长定理APOB若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明: PA,PB是⊙O的切线,点A,B是切点∴PA=PBOPA=OPB∠∠∴△PAB是等腰三角形,PM为顶角的平分线∴OP垂直平分ABM试一试试一试APO。B若延长PO交⊙O于点C,连结CA、CB,你又能得出什么新的结论?并给出证明.CA=CB证明: PA,PB是⊙O的切线,点A,B是切点∴PA=PBOPA=OPB∠∠∴PC=PC∴△PCAPCB≌△∴AC=BCC。PBAO(3)连结圆心和圆外一点(2)连结两切点(1)分别连结圆心和切点反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形。想一想想一想(2)已知OA=3cm,OP=6cm,则∠APB=PABCO60°(4)OP交⊙O于M,则,ABOPAM=BM⌒⌒M⊥牛刀小试(3)若∠P=70°,则∠AOB=°110(1)若PA=4、PM=2,求圆O的半径OAOA=3已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长。EAQPFBO易证EQ=EA,FQ=FB,PA=PB∴PE+EQ=PA=12cmPF+FQ=PB=PA=12cm∴周长为24cm牛刀再试牛刀再试探究:PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。BAPOCED(1)写出图中所有的垂直关系OAPA⊥,OBPB⊥,ABOP⊥(3)写出图中所有的全等三角形△AOP△BOP△,△AOCBOC≌△,△ACPBCP≌△(4)写出图中所有的等腰三角形△ABPAOB△(2)写出图中与∠OAC相等的角∠OAC=OBC=APC=BPC∠∠∠练习1.(口答)如图所示PA、PB分别切圆O于A、B,并与圆O的切线分别相交于C、D,已知PA=7cm,(1)求△PCD的周长.(2)如果∠P=46°,求∠COD的度数C·OPBDAE切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。APO。BECD PA、PB分别切⊙O于A、B∴PA=PB,OPA=OPB∠∠OP垂直平分AB切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。课堂小结课堂小结课堂小结课堂小结.o.o.o..o外切圆圆心:三角形三边垂直平分线的交点。外切圆的半径:交点到三角形任意一个定点的距离。三角形外接圆三角形内切圆.o内切圆圆心:三角形三个内角平分线的交点。内切圆的半径:交点到三角形任意一边的垂直距离。AABBCC例例11ABC△ABC△的内切圆⊙的内切圆⊙OO与与BCBC、、CACA、、ABAB分别相切于分别相切于点点DD、、EE、、FF,且,且AB=9cmAB=9cm,,BC=14cmBC=14cm,,CA=13cmCA=13cm,,求求AFAF、、BDBD、、CECE的长的长..解解::设设AF=x(cm),BD=y(cm),CEAF=x(cm),BD=y(cm),CE==z(cm)z(cm)∴∴AF=4(cm),BD=5(cm),CE=9(cm).AF=4(cm),BD=5(cm),CE=9(cm). ⊙⊙OO与与△△ABCABC的三边都相的三边都相切切∴∴AFAF==AE,BDAE,BD==BF,CEBF,CE==CDCD则有则有xx++yy==99yy++zz==1414xx++zz==1313解得解得xx==44yy==55zz==99练习1.如图,△ABC中,∠C=90,º它的内切圆O分别与边AB、BC、CA相切于点D、E、F,且BD=12,...