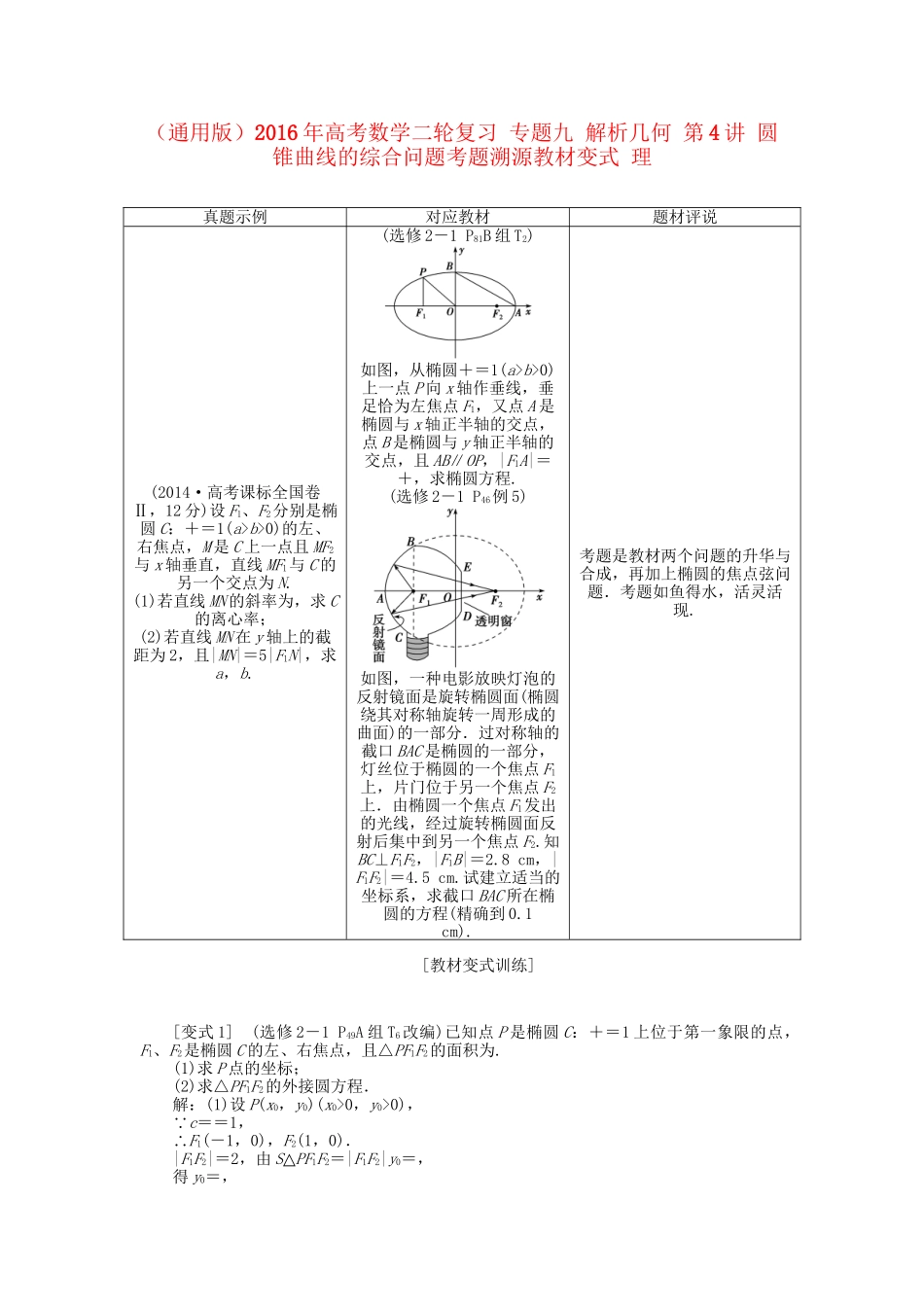
(通用版)2016年高考数学二轮复习专题九解析几何第4讲圆锥曲线的综合问题考题溯源教材变式理真题示例对应教材题材评说(2014·高考课标全国卷Ⅱ,12分)设F1、F2分别是椭圆C:+=1(a>b>0)的左、右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.(1)若直线MN的斜率为,求C的离心率;(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.(选修2-1P81B组T2)如图,从椭圆+=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,|F1A|=+,求椭圆方程.(选修2-1P46例5)如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上.由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.知BC⊥F1F2,|F1B|=2.8cm,|F1F2|=4.5cm.试建立适当的坐标系,求截口BAC所在椭圆的方程(精确到0.1cm).考题是教材两个问题的升华与合成,再加上椭圆的焦点弦问题.考题如鱼得水,活灵活现.[教材变式训练][变式1](选修2-1P49A组T6改编)已知点P是椭圆C:+=1上位于第一象限的点,F1、F2是椭圆C的左、右焦点,且△PF1F2的面积为.(1)求P点的坐标;(2)求△PF1F2的外接圆方程.解:(1)设P(x0,y0)(x0>0,y0>0), c==1,∴F1(-1,0),F2(1,0).|F1F2|=2,由S△PF1F2=|F1F2|y0=,得y0=,又+=1,∴x=5=1,∴x0=1,∴P点的坐标为.(2)显然PF2⊥x轴,∴△PF1F2的外接圆是以|F1P|为直径的圆,圆心坐标为,半径R=|F1P|==,故△PF1F2的外接圆方程为x2+=.[变式2](选修2-1P62B组T1改编)已知椭圆C1:+=1(a>b>0)与抛物线C2:y2=2px(p>0)有相同的焦点F,且它们的一个交点坐标为P(,).(1)求椭圆C1的方程与抛物线C2的方程;(2)若直线FP与抛物线的另一个交点为Q,P、Q在抛物线C2的准线上的射影分别为M、N,求梯形PMNQ的面积.解:(1)依题意得2p==4,抛物线C2方程为y2=4x,焦点F(1,0),由,解得,故椭圆C1的方程为+=1.(2)由两点式得直线FP方程为y=-2(x-1),代入y2=4x得6x2-13x+6=0,解得x=或x=,当x=时,y=-,∴Q(,-),此时|PQ|==,∴S梯形PMNQ=×|yP-yQ|=×=××=.[变式3](必修2-1P61练习T4改编;P80A组T11改编)等轴双曲线C1的中心在原点,焦点与抛物线C2:y2=2px(p>0)的焦点F重合,已知F到双曲线C1的渐近线的距离为2.(1)求C1与C2的方程;(2)过F的直线l与C1的两条渐近线在第一象限交于点M,在第四象限交于点N,求△OMN面积的取值范围.解:(1) 等轴双曲线C1的渐近线方程为y=±x,又F,∴由题意得=2,即=2,p=4.∴抛物线C2方程为y2=8x, F(2,0)也是双曲线C1的焦点,由c2=a2+b2=2a2得a2=c2=4,∴双曲线C1方程为-=1.(2)当l⊥x轴时,M(2,2),N(2,-2),|MN|=4,S△OMN=|MN|·|OF|=×4×2=8.当l与x轴不垂直时,设l:y=k(x-2),由解得M,由解得N,∴|OM|=,|ON|=, M在第一象限,N在第四象限,∴k2>1,∴S△OMN=|OM|·|ON|===8+>8,综上可知△OMN面积的取值范围为[8,∞+).[变式4](选修2-1P50B组T3改编)在矩形ABCD中,|AB|=8,|BC|=6,P、Q、R、S分别为四条边的中点,以SQ和PR所在直线分别为x轴,y轴,建立平面直角坐标系,如图所示,设M,N分别是线段OQ与线段CQ上的动点(O为坐标原点),并且满足|OM|·|NQ|=|MQ|·|CN|.(1)求直线PM与RN的交点T的轨迹方程,并说明是何种曲线;(2)当M是OQ的中点时,求△TPR的面积.解:(1)依题意设M(m,0),N(4,n),T(x,y),其中0≤m≤4,0≤n≤3, P(0,-3),R(0,3),∴由PM∥PT得,3x-m(y+3)=0,∴3m=.①由RN∥RT得(n-3)x-4(y-3)=0,∴4(n-3)=,② |OM|·|NQ|=|MQ|·|CN|,∴mn=(4-m)(3-n),即3m+4n=12,∴3m+4(n-3)=0.③将①②代入③得+=0,即+=1.它是中心在坐标原点、焦点在x轴上,长轴长为8,短轴长为6的椭圆(在第一象限的部分曲线).(2)当M为OQ中点时,m=2,n=.直线PM:3x-2y-6=0,直线RN:3x+8y-24=0,联立两式解得T(3.2,1.8...