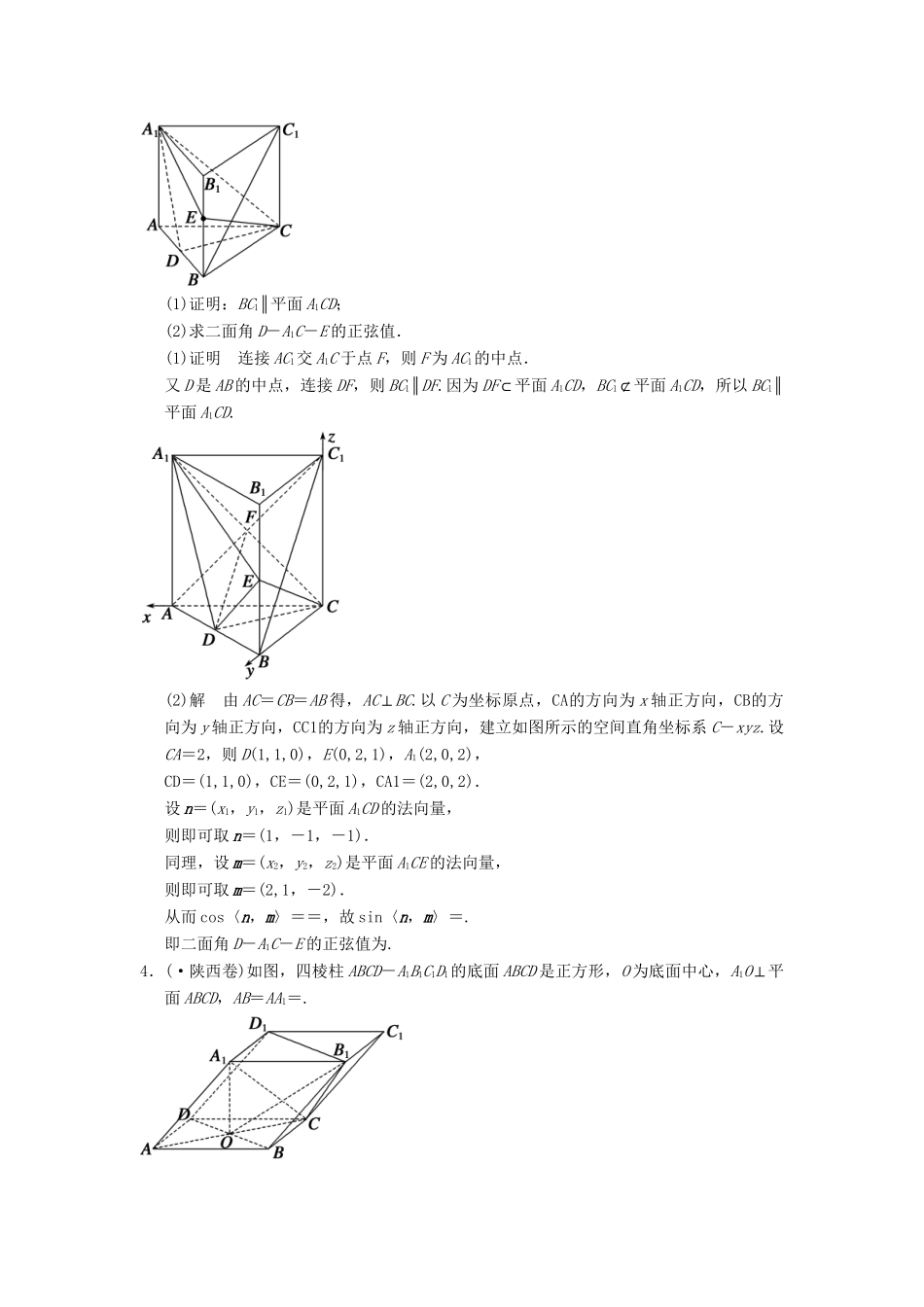
【创新设计】(江苏专用)高考数学二轮复习专题整合7-1立体几何中的向量方法(必做部分)理(含最新原创题,含解析)1.(·新课标全国卷Ⅰ)如图,三棱柱ABCA1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.(1)证明:AC=AB1;(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角AA1B1C1的余弦值.(1)证明连接BC1,交B1C于点O,连接AO.因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点.又AB⊥B1C,AB∩BO=B,所以B1C⊥平面ABO.由于AO⊂平面ABO,故B1C⊥AO.又B1O=CO,故AC=AB1.(2)解因为AC⊥AB1,且O为B1C的中点,所以AO=CO.又因为AB=BC,所以△BOA≌△BOC.故OA⊥OB,从而OA,OB,OB1两两互相垂直.以O为坐标原点,OB,OB1,OA的方向分别为x轴、y轴、z轴的正方向,|OB|为单位长,建立如图所示的空间直角坐标系O-xyz.因为∠CBB1=60°,所以△CBB1为等边三角形.又AB=BC,OC=OA,则A,B(1,0,0),B1,C.AB1=,A1B1=AB=,B1C1=BC=.设n=(x,y,z)是平面AA1B1的法向量,则即所以可取n=(1,,).设m是平面A1B1C1的法向量,则同理可取m=(1,-,).则cos〈n,m〉==.所以二面角AA1B1C1的余弦值为.2.如图,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(1)证明:AB⊥A1C;(2)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.(1)证明如图,取AB的中点O,连接CO,A1O,A1B.因为CA=CB,所以CO⊥AB,由于AA1=AB,∠BAA1=60°,故△AA1B为等边三角形,所以AB⊥A1O,因为OC∩OA1=O,所以AB⊥平面A1OC,又AC⊂平面A1OC,故AB⊥A1C.(2)解由(1)知OC⊥AB,OA1⊥AB.又平面ABC⊥平面AA1B1B,交线为AB,所以OC⊥平面AA1B1B,故OA,OA1,OC两两相互垂直.以O为原点,OA所在直线为x轴,OA1所在直线为y轴,OC所在直线为z轴,建立如图直角坐标系,则A(1,0,0),A1(0,,0),B(-1,0,0),C(0,0,),B1(-2,,0),则BC=(1,0,),BB1=(-1,,0),A1C=(0,-,),设n=(x,y,z)为平面BB1C1C的法向量,则即可取n=(,1,-1).故cos〈n,A1C〉==-.所以A1C与平面BB1C1C所成角的正弦值为.3.如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=AB.(1)证明:BC1∥平面A1CD;(2)求二面角D-A1C-E的正弦值.(1)证明连接AC1交A1C于点F,则F为AC1的中点.又D是AB的中点,连接DF,则BC1∥DF.因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.(2)解由AC=CB=AB得,AC⊥BC.以C为坐标原点,CA的方向为x轴正方向,CB的方向为y轴正方向,CC1的方向为z轴正方向,建立如图所示的空间直角坐标系C-xyz.设CA=2,则D(1,1,0),E(0,2,1),A1(2,0,2),CD=(1,1,0),CE=(0,2,1),CA1=(2,0,2).设n=(x1,y1,z1)是平面A1CD的法向量,则即可取n=(1,-1,-1).同理,设m=(x2,y2,z2)是平面A1CE的法向量,则即可取m=(2,1,-2).从而cos〈n,m〉==,故sin〈n,m〉=.即二面角D-A1C-E的正弦值为.4.(·陕西卷)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=.(1)证明:A1C⊥平面BB1D1D;(2)求平面OCB1与平面BB1D1D的夹角θ的大小.(1)证明由题设易知OA,OB,OA1两两垂直,以O为原点建立直角坐标系,如图. AB=AA1=,∴OA=OB=OA1=1,∴A(1,0,0),B(0,1,0),C(-1,0,0),D(0,-1,0),A1(0,0,1).由A1B1=AB,易得B1(-1,1,1). A1C=(-1,0,-1),BD=(0,-2,0),BB1=(-1,0,1).∴A1C·BD=0,A1C·BB1=0,∴A1C⊥BD,A1C⊥BB1,又BD∩BB1=B,∴A1C⊥平面BB1D1D.(2)解设平面OCB1的法向量n=(x,y,z). OC=(-1,0,0),OB1=(-1,1,1),∴∴取n=(0,1,-1),由(1)知,A1C=(-1,0,-1)是平面BB1D1D的法向量,∴cosθ=|cos〈n,A1C〉|==.又 0≤θ≤,∴θ=.5.(·辽宁卷)如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.(1)求证:平面PAC⊥平面PBC;(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值.(1)证明由AB是圆的直径,得AC⊥BC,由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC.又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.又BC⊂平面PBC,所以平面PBC⊥平面...