正切函数的图像与性质VIP免费

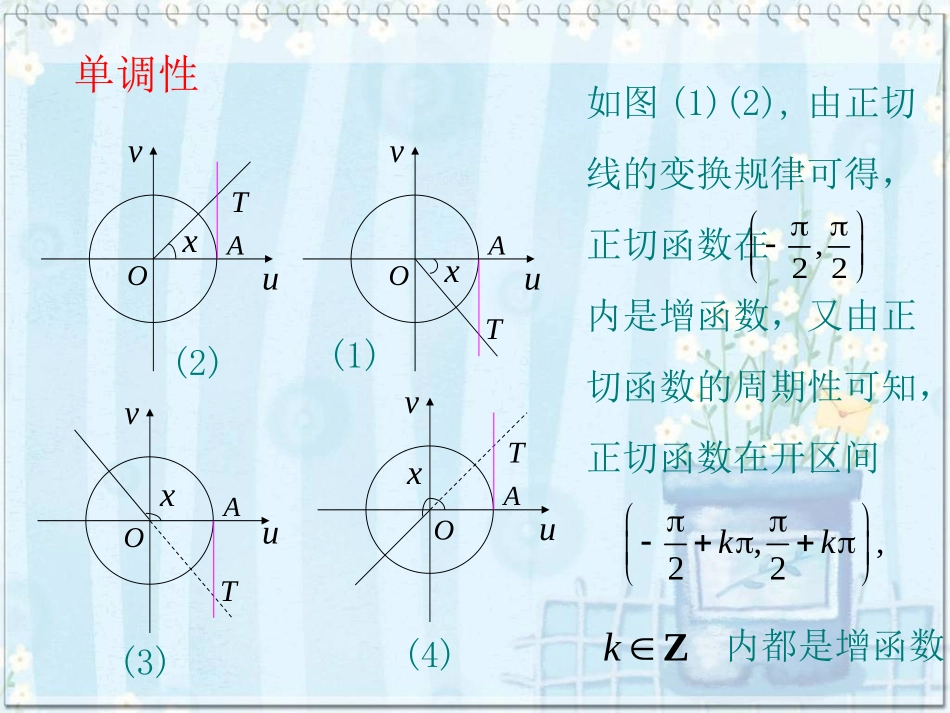
正切函数的性质与图象回顾探究试根据研究正、余弦函数的图象与性质的经验，以同样的方法研究正切函数的图象与性质.周期性tan()tan,,,2xxxxkkRZ由诱导公式得所以，正切函数是周期函数，周期是.奇偶性tan()tan,,,2xxxxkkRZ由诱导公式得所以正切函数式奇函数.单调性xuvTAOxuvTAOuxuvTAOxvTAO(1)(2)(4)(3)如图(1)(2),由正切线的变换规律可得，正切函数在内是增函数，又由正切函数的周期性可知，正切函数在开区间内都是增函数.,22,,22kkkZ值域xuTAO(1),22xATOv如图（1）当大于且无限接近时，正切线向轴的负方向无限延伸；xuvTAO(2),22xATOv如图（2）当小于且无限接近时，正切线向轴的正方向无限延伸；v所以正切函数的值域是实数集R.利用正切线画出一个周期内的正切函数图象利用正切线画出一个周期内的正切函数图象1.作直角坐标系，并在直角坐标系y轴左侧作单位圆.3.把单位圆右半圆中作出正切线并平移.4.找交叉点，用平滑的曲线把这些点连起来.XYO834884832.228x找横坐标（把轴上到这一段分成等份）作法如下：叫做正切曲线.xy0223223tan,()2yxxxkkRZ利用正切函数的周期性，把图象向左、右扩展，得到正切函数且的图象，并把它,,2xkkZ.从图中可以看出正切曲线是由被相互平行的直线所隔开的无穷多支曲线组成的全体实数R正切函数是周期函数正切函数在开区间内都是增函数。定义域值域周期性单调性正切函数性质和图象正切函数性质和图象奇偶性正切函数是奇函数，正切曲线关于原点0对称23xyo,,2xxkkRZ图象,,22kkkZ正切函数的性质与图像(,0)2k（五）定义域、值域:（六）关于对称点对称轴：从图象可以看出：无对称轴。直线为渐近线,对称点为零点及函数值不存在的点，即2xkkZ（1）正切函数在整个定义域内是增函数吗？为什么？（2）正切函数会不会在某一区间内是减函数呢？为什么？例1求函数的定义域、周期和单调区间.x解:函数的自变量应满足即所以,函数的定义域是由于因此函数的周期为2.tan23yx,232xkkZ,2,3xkkZ,2,.3xxkkZtantan2323tan2(2),23yxxxfx由解得因此,函数的单调递增区间是:,2232kxkkZ,＜＜2,33kxkkZ.＜＜22,33kkkZ.，2应用提升例1（书上P44例6有变动）tan23yx求函数的定义域，值域，并指出它的周期性，奇偶性，单调性，对称中心，作出它的大致草图Z}k312kx|{x，定义域：2T周期：Zk2k312k35），，单调区间：（R值域：奇偶性：非奇非偶解：,0),3kZ2对称中心：(k-Zkkzz,2|)4tan(xy例1求函数的定义域。,4xz解：令zytan那么函数的定义域是：kx24,4xz所以由可得：|,4xxkkZ)4tan(xy所以函数的定义域是：例2：观察正切曲线，写出满足下列条件的x的值的范围。（1）tanx>0（2）tanx<1（k，k+/2）kz（k–/2，k+/4）kzxy0–/2/2–/2xy01/2–/2/4练习：求x的范围1.tanx=02.1+tanx>03.tan(x+/4)<14.tan(3x–/3)<–1例3；比较下列各值1、tan1670与tan1730解：900〈1670〈1730〈1800又有y=tanx,在(900,2700)上是增函数所以：tan1670