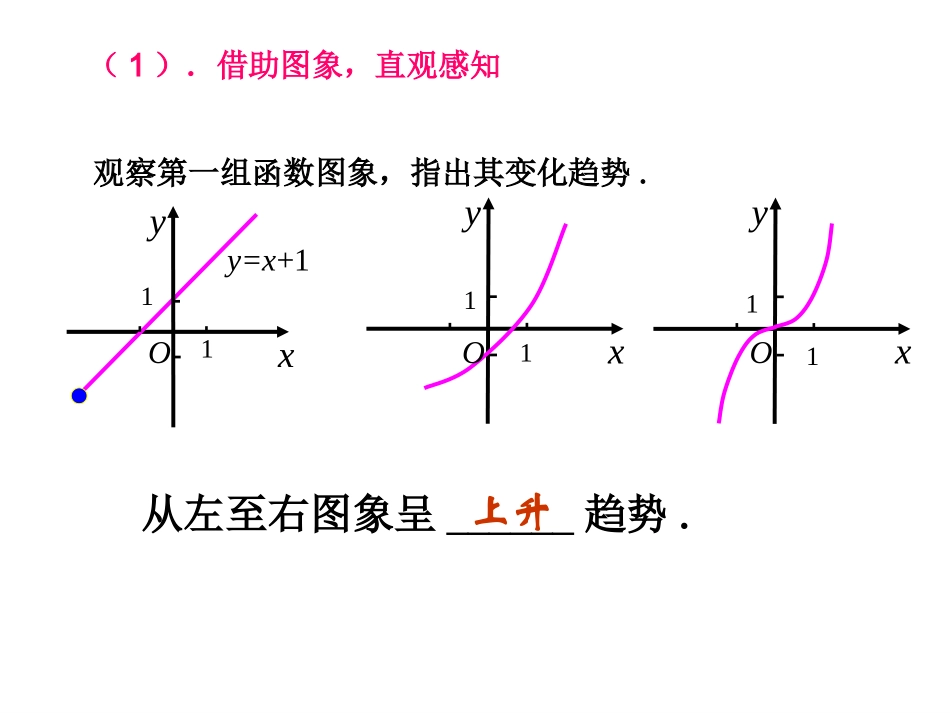
(第一教时)1、函数的单调性的定义在生活中,我们关心很多数据的变化规律,如水位高低、燃油价格、股票价格等。了解这些数据的变化规律,对我们的生活是很有帮助的.从函数观点看,其实就是研究随着自变量的变化,函数值是变大还是变小的问题。既函数的单调性问题。对于自变量变化时,函数值是变大还是变小,在初中,同学们就有了一定的认识,但是没有严格的定义,今天我们的任务首先就是建立函数单调性的严格定义.xy从左至右图象呈______趋势.上升xyy=x+1xy观察第一组函数图象,指出其变化趋势.OOO111111(1).借助图象,直观感知y=-x+1xy从左至右图象呈______趋势.下降xyxy观察第二组函数图象,指出其变化趋势.OOO111111xyy=x2y从左至右图象呈______________趋势.局部上升或下降观察第三组函数图象,指出其变化趋势.xxy11-1-1OOO1111图像从左到右逐渐上升图像从左到右逐渐下降自变量x增大,自变量x增大,在定义域内的某个区间上函数值y也增大函数值y反而减小如果函数在某个区间上随自变量x的增大,y也越来越大,我们说函数在该区间上为增函数;如果函数在某个区间上随自变量x的增大,y越来越小,我们说函数在该区间上为减函数.问题:能不能根据自己的理解说说什么是增函数、减函数?这种认识是从图象的角度得到的,是对函数单调性的直观,描述性的认识.对区间I内x1,x2,当x1减减那么就说在f(x)这个区间上是函数,I称为f(x)的单调区间.增增单调区间判断2:函数f(x)在区间[1,2]上满足f(1)<f(2),则函数f(x)在[1,2]上是增函数.()yxO12f(1)f(2)判断1:函数f(x)=x2在是单调增函数;(),xyo2yx13()(,0)(0,)(,0)(0,)fxx判断:因为函数在区间和上都是减函数,所以在上是减函数()通过判断题,强调三点:1、确定单调性一定要相对于某个区间而言,而且该区间一定要在定义域内。如y=x2只可说在(0,+∞)上为增,在R上无单调性。2、在定义中,x1、x2是任意值,不是特殊值,且同属于一个单调区间,如判断2。3、单调区间不能随便合并,两个区间之间加“,”或写“和”。如判断3。BA2、判断函数的单调性或求单调区间(1)、图像法:上升为增,下降为减()yfx例题1:根据图像指出单调增区间和单调减区间单调增区间是:单调减区间是:[2,1],[3,5][5,2],[1,3]1、函数y=x2-2|x|-3的单调递增区间;[-1,0],[1,+)-21-1oxy2223,0,23,0.xxxyxxx≥2、求函数y=|x+1|-|1-x|的单调区间.解:由y=|x+1|-|1-x|,知xy-112-2o故函数的增区间为[-1,1].1,12,2,,2,11.xxxyx≤≤小结1、函数单调性的定义2、判断函数单调性或求单调区间的方法:(1)图象法画出函数图象,再观察图象,上升为增,下降为减28302212234P优化方案例和跟踪训练,(),()P当堂检测作、:、业(第二教时)一、复习回顾:1、函数单调性的定义画出函数图象,再观察图象,上升为增,下降为减1112()()()xxfxfxfxI当时,都有在区间上为增函数;1112()()()xxfxfxfxI当时,都有在区间上为减函数;12Ixx在区间上任取、,2、判断函数单调性或求单调区间的方法:(1)图象法强调三点:1、确定单调性一定要相对于某个区间而言,而且该区间一定要在定义域内。2、在定义中,x1、x2是任意值,不是特殊值,且同属于一个单调区间。3、单调区间不能随便合并,两个区间之间不能用并集符号,应加“,”或写“和”。283022...