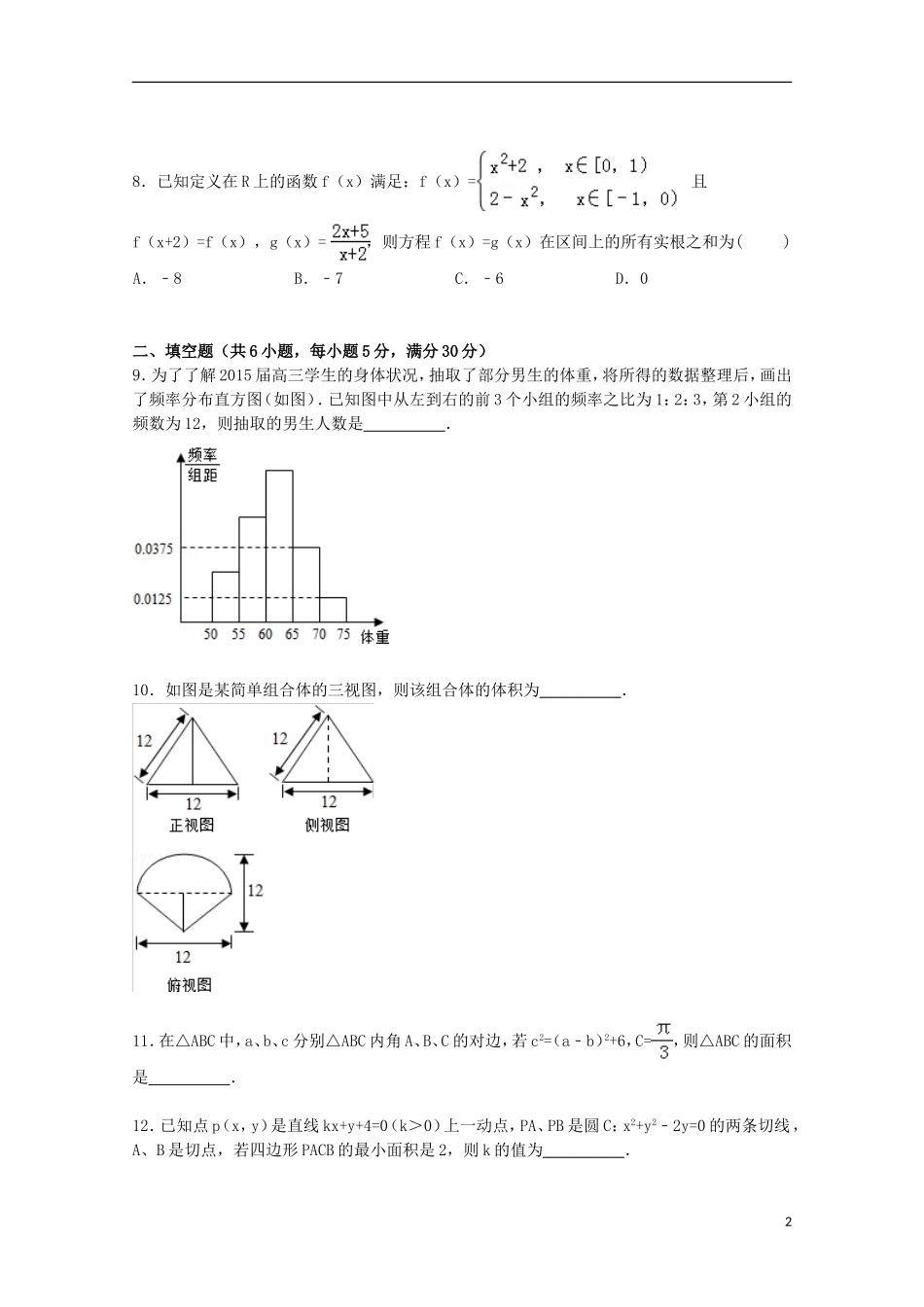
天津市耀华中学2015届高考数学二模试卷(文科)一.选择题:共8个小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题目要求的.1.复数z=在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.△ABC中,“A>”是“sinA>”的()A.必要不充分条件B.充分必要条件C.充分不必要条件D.既不充分也不必要条件3.已知变量x、y满足约束条件,若目标函数z=ax+y仅在点(3,0)处取到最大值,则实数a的取值范围()A.(,+∞)B.(﹣∞,)C.(,+∞)D.(,+∞)4.为了得到函数y=sin(2x﹣)的图象,可以将函数y=cos2x的图象()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度5.数列{an}满足a1=1,a2=,并且an(an﹣1+an+1)=2an+1an﹣1(n≥2),则该数列的第2015项为()A.B.C.D.6.设直线l:y=2x+2,若l与椭圆x2+=1的交点为A、B,点P为椭圆上的动点,则使△PAB的面积为﹣1的点P的个数为()A.0B.1C.2D.37.已知函数f(x)满足f(x)=x2﹣2(a+2)x+a2,g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max(p,q)表示p,q中的较大值,min(p,q)表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=()A.a2﹣2a﹣16B.a2+2a﹣16C.﹣16D.1618.已知定义在R上的函数f(x)满足:f(x)=且f(x+2)=f(x),g(x)=,则方程f(x)=g(x)在区间上的所有实根之和为()A.﹣8B.﹣7C.﹣6D.0二、填空题(共6小题,每小题5分,满分30分)9.为了了解2015届高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是__________.10.如图是某简单组合体的三视图,则该组合体的体积为__________.11.在△ABC中,a、b、c分别△ABC内角A、B、C的对边,若c2=(a﹣b)2+6,C=,则△ABC的面积是__________.12.已知点p(x,y)是直线kx+y+4=0(k>0)上一动点,PA、PB是圆C:x2+y2﹣2y=0的两条切线,A、B是切点,若四边形PACB的最小面积是2,则k的值为__________.213.若至少存在一个x>0,使得关于x的不等式x2<2﹣|x﹣a|成立,则实数a的取值范围为__________.14.设O是△ABC的外心,a、b、c分别为△ABC内角A、B、C的对边,且b2﹣2b+c2=0,则•的取值范围是__________.三.解答题:共6个小题,总计80分,解答应写出必要的文字说明、证明过程或演算步骤.15.已知函数.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值及取得最值时x的值.16.袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子随机抽取1个小球,取到标号为2的小球的概率是.(Ⅰ)求n的值;(Ⅱ)从袋子中不放回地随机抽取2个球,记第一次取出的小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;②在区间内任取2个实数x,y,求事件“x2+y2>(a﹣b)2恒成立”的概率.17.已知在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.(Ⅰ)求证:AF∥平面PEC;(Ⅱ)求PC与平面ABCD所成角的正弦值;(Ⅲ)求二面角P﹣EC﹣D的余弦值.18.已知函数f(x)=log3(ax+b)的图象经过点A(2,1)和B(5,2),记an=3f(n),n∈N*(1)求数列{an}的通项公式;(2)设,Tn=b1+b2+…bn,若Tn<m(m∈Z),求m的最小值;(3)求使不等式≥对一切n∈N*,均成立的最大实数p.319.已知中心在原点O,焦点在x轴上,离心率为的椭圆过点(,).(1)求椭圆的方程;(2)设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.20.已知函数f(x)=ex(其中e为自然对数的底数),g(x)=x+m(m,n∈R).(1)若T(x)=f(x)g(x),m=1﹣,求T(x)在上的最大值;(2)若n=4时方程f(x)=g(x)在上恰有两个相异实根,求m的取值范围;(3)若m=﹣...