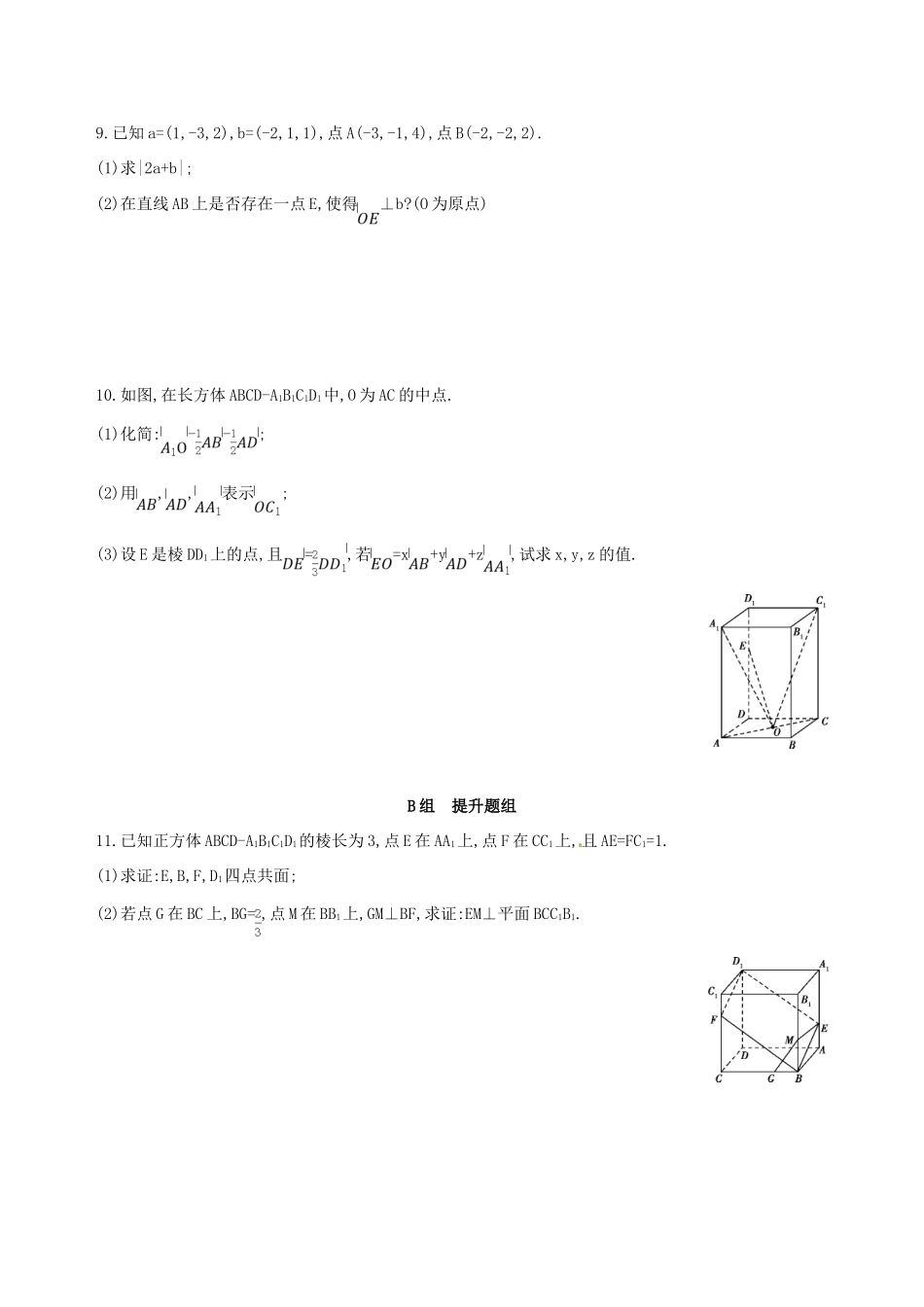
第五节空间向量及其运算A组基础题组1.若直线l的方向向量为a=(1,0,2),平面α的法向量为n=(-2,0,-4),则()A.l∥αB.l⊥αC.lα⊂D.l与α斜交2.已知a=(1,0,1),b=(x,1,2),且a·b=3,则向量a与b的夹角为()A.B.C.D.3.(2017武汉三中月考)在空间直角坐标系中,已知A(1,-2,1),B(2,2,2),点P在z轴上,且满足|PA|=|PB|,则P点坐标为()A.(3,0,0)B.(0,3,0)C.(0,0,3)D.(0,0,-3)4.对于空间一点O和不共线的三点A,B,C,有6=+2+3,则()A.O,A,B,C四点共面B.P,A,B,C四点共面C.O,P,B,C四点共面D.O,P,A,B,C五点共面5.如图,在大小为45°的二面角A-EF-D中,四边形ABFE,CDEF都是边长为1的正方形,则B,D两点间的距离是()A.B.C.1D.6.已知a=(2,4,x),b=(2,y,2),若|a|=6,且a⊥b,则x+y的值为.7.已知V为矩形ABCD所在平面外一点,且VA=VB=VC=VD,=,=,=.则VA与平面PMN的位置关系是.8.如图,已知P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点M在线段PC上,点N在线段PD上,且PM=2MC,PN=ND,若=x+y+z,则x+y+z=.9.已知a=(1,-3,2),b=(-2,1,1),点A(-3,-1,4),点B(-2,-2,2).(1)求|2a+b|;(2)在直线AB上是否存在一点E,使得⊥b?(O为原点)10.如图,在长方体ABCD-A1B1C1D1中,O为AC的中点.(1)化简:--;(2)用,,表示;(3)设E是棱DD1上的点,且=,若=x+y+z,试求x,y,z的值.B组提升题组11.已知正方体ABCD-A1B1C1D1的棱长为3,点E在AA1上,点F在CC1上,且AE=FC1=1.(1)求证:E,B,F,D1四点共面;(2)若点G在BC上,BG=,点M在BB1上,GM⊥BF,求证:EM⊥平面BCC1B1.12.如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.求证:(1)CM∥平面PAD;(2)平面PAB⊥平面PAD.答案全解全析A组基础题组1.B∵a=(1,0,2),n=(-2,0,-4),∴n=-2a,即a∥n,∴l⊥α.2.D∵a·b=x+2=3,∴x=1,∴b=(1,1,2).∴cos
===.∴a与b的夹角为,故选D.3.C设P(0,0,z),则有=,解得z=3.故选C.4.B由6=+2+3,得-=2(-)+3(-),即=2+3,故,,共面,又它们有公共点P,因此,P,A,B,C四点共面,又O不一定与P,A,B,C共面,故选B.5.D∵=++,∴||2=||2+||2+||2+2·+2·+2·=1+1+1-=3-,∴||=.6.答案1或-3解析由|a|=6,得=6,解得x=±4,因为a⊥b,所以2×2+4y+2x=0,即x+2y=-2.当x=4时,y=-3,所以x+y=1;当x=-4时,y=1,所以x+y=-3.综上,x+y=1或-3.7.答案平行解析如图,设=a,=b,=c,则=a+c-b,由题意知=b-c,=-=a-b+c,因此=+,∴,,共面.又∵VA⊄平面PMN,∴VA∥平面PMN.8.答案-解析=-=-=(-)-(+)=-+-(+)=--+,所以x+y+z=--+=-.9.解析(1)2a+b=(2,-6,4)+(-2,1,1)=(0,-5,5),故|2a+b|==5.(2)由题意,令=t(t∈R),所以=+=+t=(-3,-1,4)+t(1,-1,-2)=(-3+t,-1-t,4-2t),若⊥b,则·b=0,所以-2(-3+t)+(-1-t)+(4-2t)=0,解得t=.因此在直线AB上存在点E,使得⊥b,此时E点的坐标为.10.解析(1)因为+=,所以--=-(+)=-=-=.(2)=+=+=(+)+=++.(3)因为=+=+=+(+)=++=--,所以x=,y=-,z=-.B组提升题组11.证明(1)以B为原点,以BA,BC,BB1所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系B-xyz,则B(0,0,0),E(3,0,1),F(0,3,2),D1(3,3,3),则=(3,0,1),=(0,3,2),=(3,3,3),所以=+.由向量共面的充要条件知E,B,F,D1四点共面.(2)易知G,设M(0,0,z0),则=,又=(0,3,2),则由题设得·=-×3+z0·2=0,得z0=1.故M(0,0,1),所以=(3,0,0).又=(0,0,3),=(0,3,0),所以·=0,·=0.从而ME⊥BB1,ME⊥BC.又BB1∩BC=B,故ME⊥平面BCC1B1.12.证明以C为坐标原点,CB所在直线为x轴,CD所在直线为y轴,CP所在直线为z轴建立如图所示的空间直角坐标系C-xyz.∵PC⊥平面ABCD,∴∠PBC为PB与平面ABCD所成的角,∴∠PBC=30°,∵PC=2,∴BC=2,PB=4.易得D(0,1,0),B(2,0,0),A(2,4,0),P(0,0,2),M,∴=(0,-1,2),=(2,3,0),=.(1)设n=(x,y,z)为平面PAD的法向量,则即令y=2,得n=(-,2,1).∵n·=-×+2×0+1×=0,∴n⊥.又CM⊄平面PAD,∴CM∥平面PAD.(2)证法一:易知=(0,4,0),=(2,0,-2),设平面PAB的法向量为m=(x0,y0,z0),则即令x0=1,得m=(1,0,),又∵平面PAD的一个法向量为n=(-,2,1),∴m·n=1×(-)+0×2+×1=0,∴平面PAB⊥平面PAD.证法二:如图,取AP的中点E,连接BE,则E(,2,1),=(-,2,1).∵PB=AB,∴BE⊥PA.又∵·=(-,2,1)·(2,3,0)=0,∴⊥.∴BE⊥DA.又PA∩DA=A,∴BE⊥平面PAD.又∵BE⊂平面PAB,∴平面PAB⊥平面PAD.