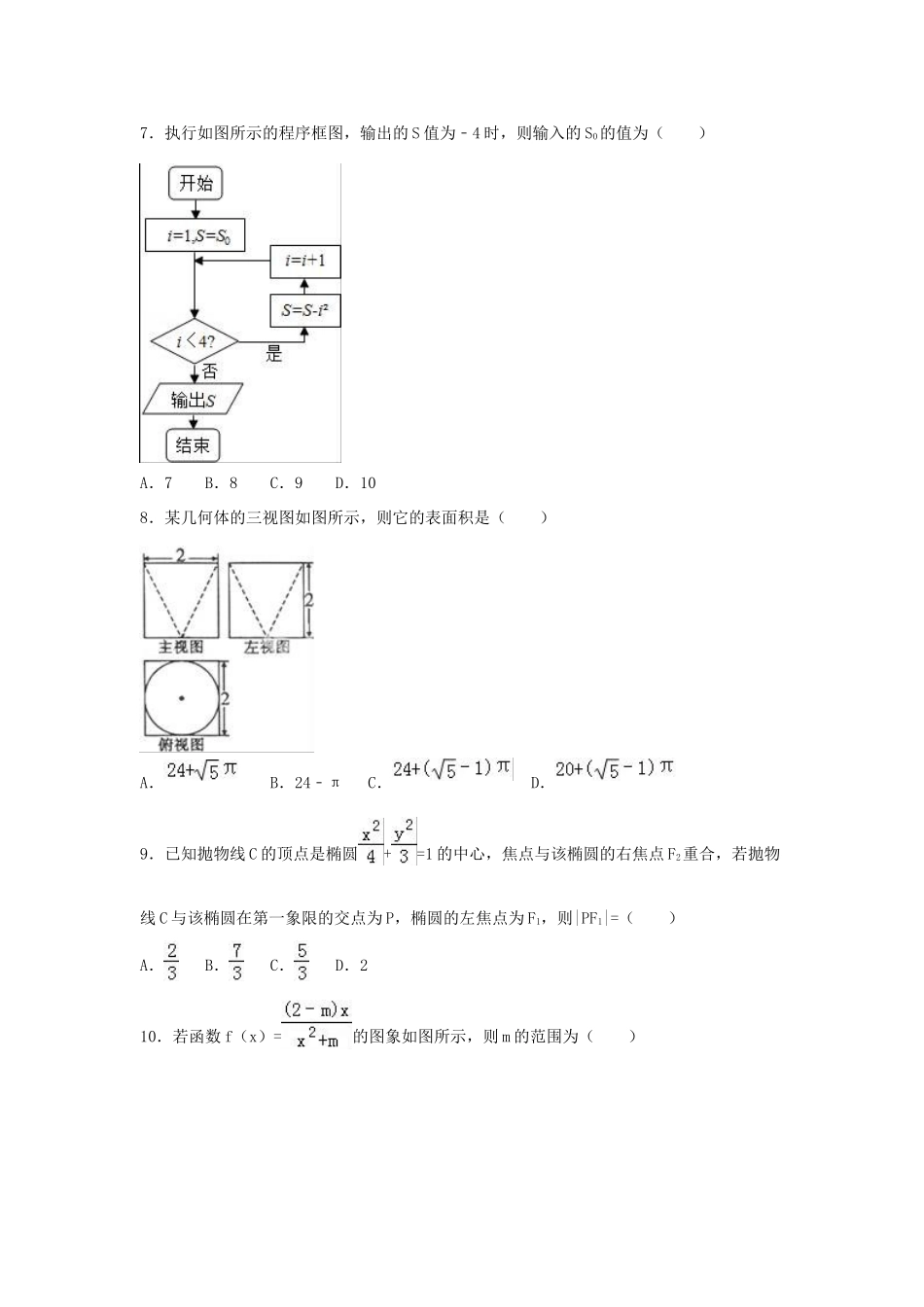
2016年安徽省池州市高考数学二模试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={0,1,2},B={x|x2﹣x﹣2<0},则A∩B=()A.{0,1,2}B.{1,2}C.{0,1}D.{0}2.设i是虚数单位,复数z满足z(1+i)=2i,则复数z的虚部为()A.﹣iB.iC.1D.﹣13.双曲线﹣y2=1的焦点F到其渐近线的距离为()A.B.1C.D.24.元宵节晚上有三支龙灯表演队,甲、乙两位志愿者各自参加其中一支表演队,每一位志愿者参加各支表演队的可能性相同,则这两位志愿者参加同一支表演队的概率为()A.B.C.D.5.已知sin(π+α)=,则sin(+2α)=()A.B.﹣C.﹣D.6.已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,在x轴上的投影为,则的值为()A.B.C.D.7.执行如图所示的程序框图,输出的S值为﹣4时,则输入的S0的值为()A.7B.8C.9D.108.某几何体的三视图如图所示,则它的表面积是()A.B.24﹣πC.D.9.已知抛物线C的顶点是椭圆+=1的中心,焦点与该椭圆的右焦点F2重合,若抛物线C与该椭圆在第一象限的交点为P,椭圆的左焦点为F1,则|PF1|=()A.B.C.D.210.若函数f(x)=的图象如图所示,则m的范围为()A.(﹣∞,﹣1)B.(﹣1,2)C.(0,2)D.(1,2)11.若变量x,y满足z=+(a≥b>0)的最大值2,则有()A.ab﹣3a﹣b=0B.ab﹣a﹣3b=0C.ab﹣a﹣b=0D.ab+a﹣b=012.设函数f′(x)是偶函数f(x)(x∈R)的导函数,f(x)在区间(0,+∞)上的唯一零点为2,并且当x∈(﹣1,1)时,xf′(x)+f(x)<0.则使得f(x)<0成立的x的取值范围是()A.(﹣2,0)∪(0,2)B.(﹣∞,﹣2)∪(2,+∞)C.(﹣1,1)D.(﹣2,2)二、填空题(本大题共4小题,每小题5分,共20分)13.如图,,为互相垂直的两个单位向量,则向量+可用,表示为.14.如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h′(1)=.15.△ABC的内角A、B、C所对的边分别为a、b、c,若a=1,b+c=,且cosA=,则△ABC的面积为.16.表面积为60π的球面上有四点S、A、B、C,且△ABC是等边三角形,球心O到平面ABC的距离为,若平面SAB⊥平面ABC,则棱锥S﹣ABC体积的最大值为.三、解答题(本大题共5小题,共70分,解答应写出文字说明、演算步骤或证明过程.)17.已知公差不为零的等差数列{an}的前n项和为Sn,满足a1=﹣1,且a2,a3,a6成等比数列.(Ⅰ)求an及Sn;(Ⅱ)设bn=,求数列{bn}的前n项和Tn.18.如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC=2(I)求证:AC⊥CD;(Ⅱ)点E在棱PC的中点,求点B到平面EAD的距离.19.近年来空气污染是生活中一个重要的话题,PM2.5就是空气质量的其中一个重要指标,各省、市、县均要进行实时监测.空气质量指数要求PM2.524小时浓度均值分:估[0,35]、良(35,75],轻度污染(75,115],中度污染根据数据绘制频率分布表,并求PM2.524小时浓度均值的中位数;空气质量指数类别频数频率优[0,35]良(35,75]轻度污染(75,115]中度污染(115,150]重度污染(150,250]严重污染(250,500]合计301(Ⅱ)专家建议,空气质量为优、良、轻度污染时可以正常进行户外活动,中度污染及以上时,取消一切户外活动.池州市某家庭准备在2016年2月1日至3月1日间连续两天在外郊游(假设数据为出游前的预报数据),家庭考虑小孩的因素,选择空气质指数为优时出游,求该家庭外出郊游的概率.20.已知圆O:x2+y2=1的切线l与椭圆C:x2+3y2=4相交于A、B、两点.(Ⅰ)求椭圆C的离心率;(Ⅱ)求证:OA⊥OB.21.已知函数f(x)=x2﹣(﹣1)n2alnx(n∈Z,a>0).(Ⅰ)求函数f(x)的极值;(Ⅱ)若n=2016,且函数y=2ax﹣f(x)有唯一零点x0,求x0与a.请考生在22-24三题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-1:几何证明选讲]22.如图,AB...