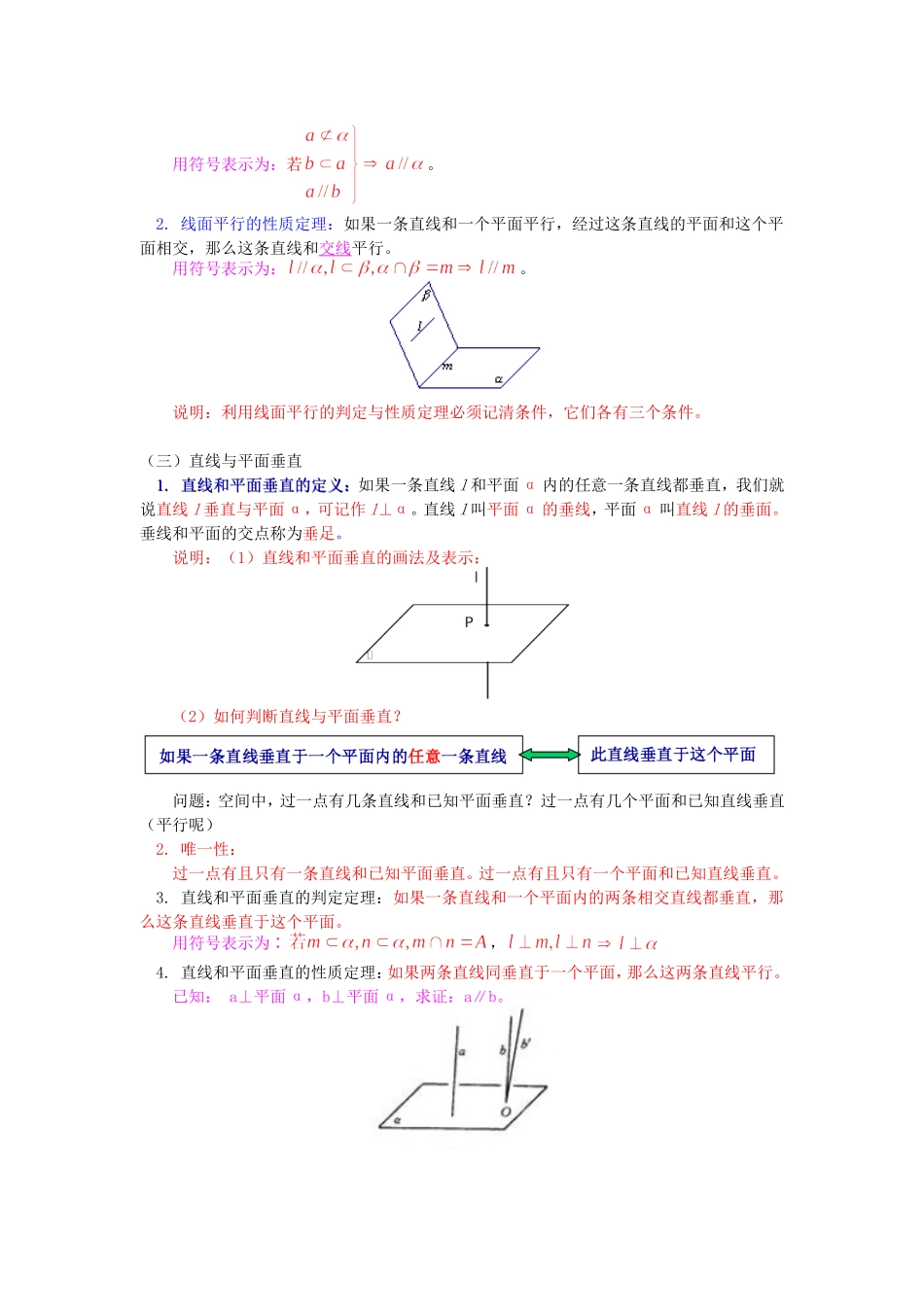
高一数学直线与平面的位置关系苏教版【本讲教育信息】一.教学内容:直线与平面的位置关系二.本周教学目标:1、了解直线和平面的位置关系种类;掌握直线和平面平行的判定、性质定理,及能进行证明运用。2、了解直线和平面垂直的定义及相关概念;掌握直线和平面垂直的判定定理与性质定理,及能进行证明运用。3、理解并掌握斜线在平面内的射影、直线和平面所成角的概念,能根据概念先找直线射影后确定线面夹角从而熟练求解直线和平面所成角。三、知识要点:(一)直线和平面的位置关系:问:给定一条直线与一个平面,则这条直线与平面具有的公共点的个数可能有几种情况如果一条直线和一个平面没有公共点,那么我们说这条直线和这个平面平行。如果一条直线和一个平面有且只有一个公共点,那么我们说这条直线和这个平面相交。如果一条直线和一个平面有无数个公共点,那么我们说这条直线在这个平面内。1.归纳:一条直线和一个平面的位置关系有且只有以下三种:(1)直线在平面内—有无数个公共点。(2)直线和平面相交—有且只有一个公共点。(3)直线和平面平行—无公共点。我们把直线和平面相交或平行的情况统称为在平面外。它们的图形分别可表示为如下,符号分别可表示为,,。aaAa2.直线和平面的三种位置关系的画法:(二)直线与平面平行1.1.线面平行的判定定理:线面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。用符号表示为:若。2.线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。用符号表示为:。说明:利用线面平行的判定与性质定理必须记清条件,它们各有三个条件。(三)直线与平面垂直1.1.直线和平面垂直的定义:直线和平面垂直的定义:如果一条直线l和平面α内的任意一条直线都垂直,我们就说直线l垂直与平面α,可记作l⊥α。直线l叫平面α的垂线,平面α叫直线l的垂面。垂线和平面的交点称为垂足。说明:(1)直线和平面垂直的画法及表示:(2)如何判断直线与平面垂直?问题:空间中,过一点有几条直线和已知平面垂直?过一点有几个平面和已知直线垂直(平行呢)2.唯一性:过一点有且只有一条直线和已知平面垂直。过一点有且只有一个平面和已知直线垂直。3.直线和平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。用符号表示为∶,4.直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。已知:a⊥平面α,b⊥平面α,求证:a∥b。(四)直线与平面所成的角观察立方体,可以发现AB1,A1C,A1D虽都与平面ABCD相交,但都不垂直。1.斜线、垂线、射影(1)垂线:自一点向平面引垂线,垂足叫这点在这个平面上的射影。这个点和垂足间的线段叫做这点到这个平面的垂线段。(2)斜线:一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线斜线和平面的交点叫斜足;斜线上一点与斜足间的线段叫这点到这个平面的斜线段。(3)射影:如图,过平面外一点A向平面引斜线和垂线,那么过斜足B和垂足O的直线就是斜线在这个平面内的射影。线段BO就是斜线段AB在平面内的射影。说明:直线与平面平行,直线在平面的射影是一条直线;直线与平面垂直射影是点;斜线任一点在平面内的射影一定在斜线的射影上。2.射影长相等定理:从平面外一点向这个平面所引的垂线段和斜线段中⑴射影相交两条斜线相交;射影较长的斜线段也较长。⑵相等的斜线段射影相等;较长的斜线段射影较长。⑶垂线段比任何一条斜线段都短。3.直线和平面所成角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角。一直线垂直于平面,所成的角是直角。一直线平行于平面或在平面内,所成角为0角直线和平面所成角范围:,【典型例题】例1.如果三个平面两两相交于三条直线,并且其中两条直线平行,那么第三条直线也和它们平行。例2.在如图所示的一块木料中,棱BC平行于面A’C’,(1)要经过面A’C’内的一点P和棱BC将木料锯开,应怎样画线?(2)所画的线和面AC是什...