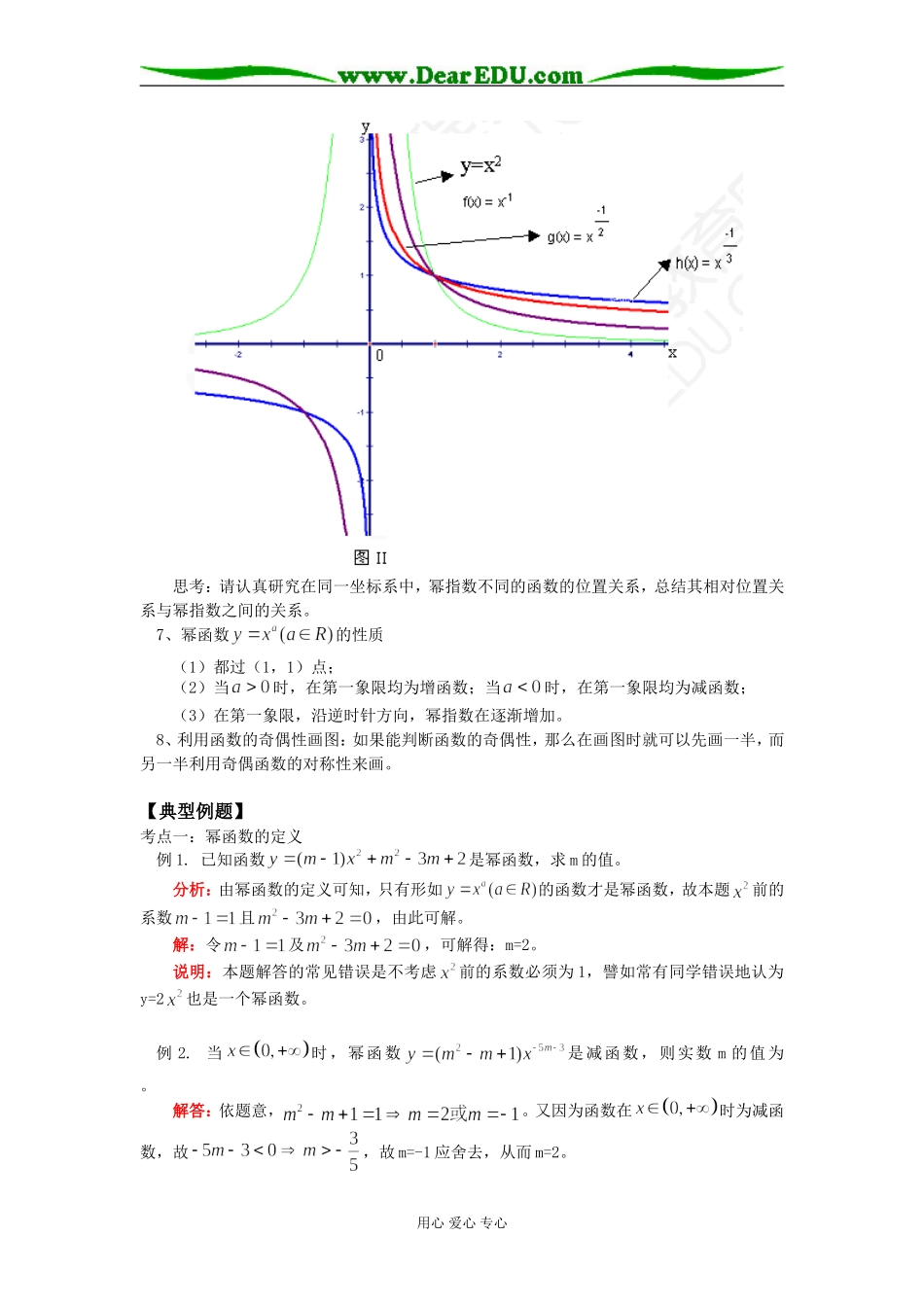
高一数学幂指对数函数(一)北师大版【本讲教育信息】一.教学内容:幂指对数函数(一)简单的幂函数与函数的奇偶性二.学习目标1、了解指数是整数的简单幂函数的概念;2、会用定义法证明简单函数的奇偶性;3、了解利用奇偶性画函数图像和研究函数的方法;4、进一步研究函数的单调性;5、培养从特殊归纳出一般的意识,学习利用图像研究函数奇偶性等能力三.知识要点1、幂函数:形如的函数称为幂函数,如我们熟悉的正比例函数,反比例函数和二次函数等。2、奇函数:一般地,图像关于原点对称的函数叫作奇函数。。3、偶函数:一般地,图像关于y轴对称的函数叫作偶函数。。4、函数的奇偶性:当函数是奇函数或者是偶函数时,称函数具有奇偶性,从而函数的奇偶性有四种情形:奇函数、偶函数、既奇又偶函数(如y=0)、非奇非偶函数。5、判断函数奇偶性的一般步骤:I、判断定义域关于原点是否对称;II、判断的关系;III、根据定义给出结论。6、在同一坐标系中画出不同的幂函数的图像:图I用心爱心专心思考:请认真研究在同一坐标系中,幂指数不同的函数的位置关系,总结其相对位置关系与幂指数之间的关系。7、幂函数的性质(1)都过(1,1)点;(2)当时,在第一象限均为增函数;当时,在第一象限均为减函数;(3)在第一象限,沿逆时针方向,幂指数在逐渐增加。8、利用函数的奇偶性画图:如果能判断函数的奇偶性,那么在画图时就可以先画一半,而另一半利用奇偶函数的对称性来画。【典型例题】考点一:幂函数的定义例1.已知函数是幂函数,求m的值。分析:由幂函数的定义可知,只有形如的函数才是幂函数,故本题前的系数且,由此可解。解:令及,可解得:m=2。说明:本题解答的常见错误是不考虑前的系数必须为1,譬如常有同学错误地认为y=2也是一个幂函数。例2.当时,幂函数是减函数,则实数m的值为。解答:依题意,。又因为函数在时为减函数,故,故m=-1应舍去,从而m=2。用心爱心专心考点二:判断函数的奇偶性一般地,判断函数的奇偶性首先应确认函数的定义域关于原点对称,然后再根据f(x)和f(-x)的关系进行判断,若相等,则为偶函数;若相反,则为奇函数。也可以根据图像的对称性来判断:若图像关于原点对称,则为奇函数;若图像关于y轴对称,则为偶函数。例3.判断函数的奇偶性。解答:因为函数的定义域是{x|x≠1},关于原点不对称,所以该函数为非奇非偶函数。说明:若将此函数先化简得到f(x)=-x,则极易得到该函数是奇函数这样一个错误的结论;另外,本题最后的结论是该函数是非奇非偶函数,不可以说成“不具有奇偶性”。例4.判断函数的奇偶性。解答:说明:分段函数的奇偶性的判断是一个难点,要注意分段进行判断,并要注意是将f(-x)和哪个区间上的f(x)进行比较。考点三:复合函数的奇偶性复合函数y=f[g(x)]的奇偶性可以这样判断:当内外函数均为奇函数时,复合函数是奇函数;当内外函数中有一个是偶函数,而另一个函数无论是奇函数或偶函数,复合函数均为偶函数。例5.判断函数的奇偶性。解答:设,则g(x)是偶函数;又因为可视为的复合函数,故为偶函数。考点四:利用函数的奇偶性解题例6.已知函数是奇函数,当x>0时,;求当x<0时的解析式。解答:说明:这个例题十分典型,请同学们认真体会其做法。例7.试探究是否存在实数,使得函数是奇函数?若存在,求出实数,并证明函数是奇函数;若不存在,请说明理由。解答:函数的定义域是(-1,1),若函数是奇函数,必有f(0)=0,解得用心爱心专心,易证这是一个奇函数。说明:若奇函数在x=0时有意义,则必有f(0)=0。(同学们不妨证明一下这个结论)考点五:幂函数的图像例8.函数的图像是()解答:由是偶函数,排除B、C;又当0x,故选D。考点六:比较大小例9.比较下列两式的大小;;解答:画出的图像,由于函数当x>0时是一个增函数,故;在同一坐标系中画出的图像,故有;由于,故有:。说明:比较这类式子的大小时,往往要充分利用幂函数的单调性以及在同一坐标系中不同指数的幂函数的图像的相互位置关系进行判断。用心爱心专心考点七:解不等式例10.解不等式。解答:由于是一个增函数,故由知:,...