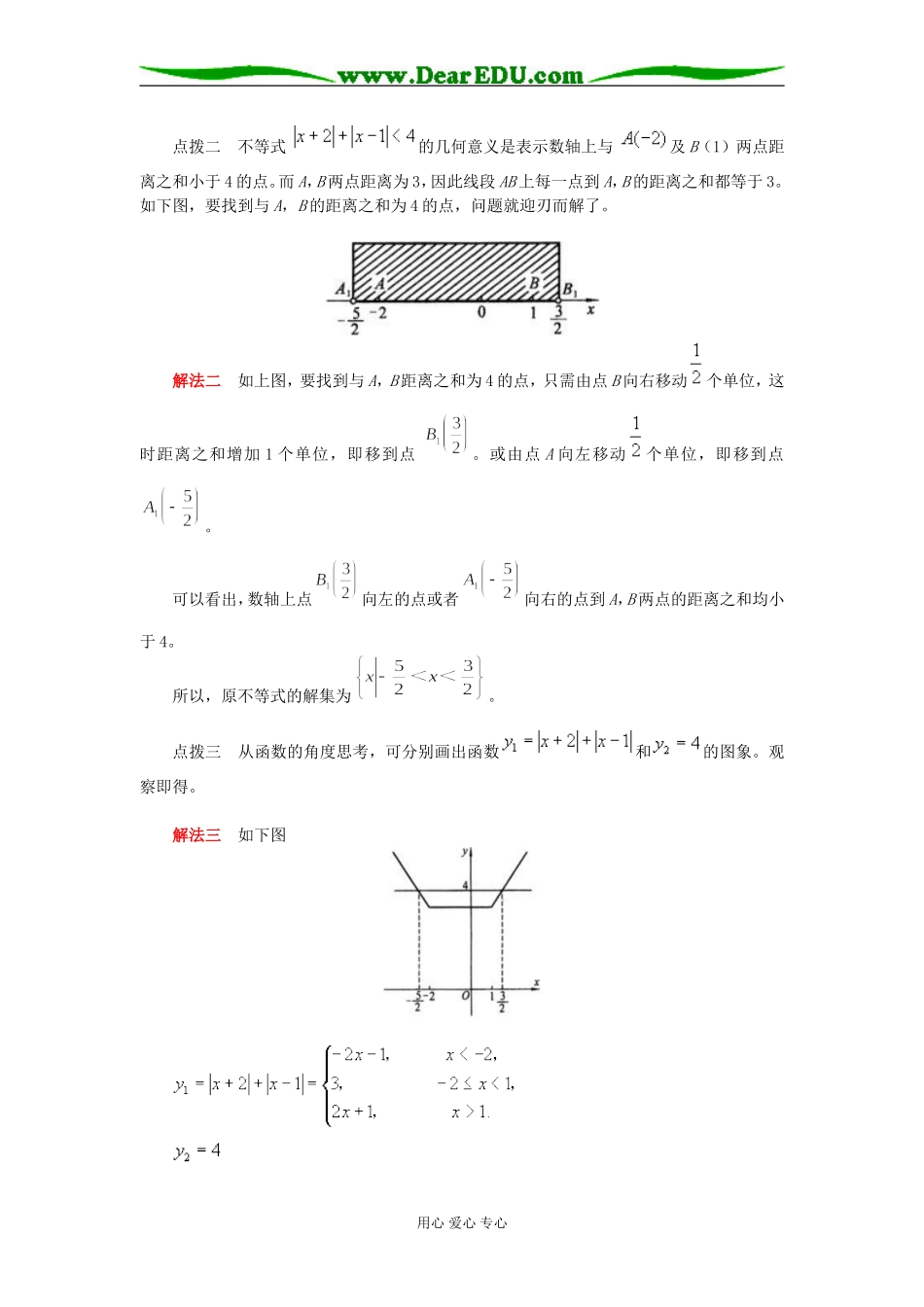
高一数学两种不等式的解法【本讲主要内容】两种不等式的解法绝对值不等式、一元二次不等式的解法【知识掌握】【知识点精析】1.的解集是;2.的解集是解绝对值不等式时要注意不要丢掉这部分解集。或型的绝对值不等式,若把看成一个整体一个字母,就可以归结为或型绝对值不等式的解法。3.一元二次不等式的解法:一般地,对于一元二次方程ax2+bx+c=0(a>0),△=b2-4ac,(1)△>0时,方程ax2+bx+c=0(a>0)的两个根为:x1,x2,设x10的解集是:{x∣xx2}一元二次不等式ax2+bx+c<0的解集是:{x∣x10)的两个根为:x1=x2一元二次不等式ax2+bx+c>0的解集是:{x∣x≠x1}一元二次不等式ax2+bx+c<0的解集是:。(3)△<0时,方程ax2+bx+c=0(a>0)无实根,一元二次不等式ax2+bx+c>0的解集是:实数集R一元二次不等式ax2+bx+c<0的解集是:【解题方法指导】例1.解不等式()分析:此题关键在于绝对值符号里有字母系数,解题过程中要注意分类讨论.用心爱心专心解:原不等式可化为即当时,解集为当时,解集为评析:1.遇到字母系数要合理进行讨论,尤其是字母系数为负时,利用不等式性质化简不等式时一定要改变不等号的方向。2.若遇的系数为负的含绝对值不等式,如,等,可利用绝对值的性质将其转化为系数为正的情况去解,如将上述两不等式变为,后再解,以减小错误的发生率。例2.解不等式点拨一这是一个含有两个绝对值的符号的不等式,为了使其转化为解不含绝对值符号的不等式,要进行分类讨论。解法一由代数式,知,-2,1把实数集分为三个区间:,,。当时,原不等式变为,即;当时,原不等式变为,即;当时,原不等式变为,即。综上,知原不等式的解集为。点评解这类绝对值符号里是一次式的不等式,其一般步骤是:(1)令每个绝对值符号里的一次式为零,求出相应的根;(2)把这些根由小到大排序并把实数集分为若干个区间;(3)由所分区间去掉绝对值符号组成若干个不等式,解这些不等式,求出它们的解集;(4)这些不等式的解集的并集就是原不等式的解集。用心爱心专心点拨二不等式的几何意义是表示数轴上与及B(1)两点距离之和小于4的点。而A,B两点距离为3,因此线段AB上每一点到A,B的距离之和都等于3。如下图,要找到与A,B的距离之和为4的点,问题就迎刃而解了。解法二如上图,要找到与A,B距离之和为4的点,只需由点B向右移动个单位,这时距离之和增加1个单位,即移到点。或由点A向左移动个单位,即移到点。可以看出,数轴上点向左的点或者向右的点到A,B两点的距离之和均小于4。所以,原不等式的解集为。点拨三从函数的角度思考,可分别画出函数和的图象。观察即得。解法三如下图用心爱心专心不难看出,要使,只须。所以,原不等式的解集为。点评对于解法一,要熟记或两种类型的解法,关键是正确分类并转化为不含绝对值的不等式;对于解法二,要搞清它的几何意义是什么,并注意结论是否包括端点;对于解法三,关键是正确画出两个函数的图象,并准确写出它们交点的坐标。三种方法都比较直观、简捷,不同程度体现了分类讨论、函数与方程、数形结合等数学思想方法,各有千秋,都是我们应该熟练掌握的解题通性通法。例3.解不等式(为参数)分析:这是一个含有字母的一元二次不等式,在解题时要注意对字母的讨论。解:原不等式可化为若,则,即,原不等式的解集为;若,即或,则原不等式的解集为;若,即或,则原不等式的解集为因此,当时,原不等式的解集为;当或时,原不等式的解集为说明:此题是带字母问题,要涉及到分类讨论问题。讨论中又涉及到解二次不等式,所用到的知识比较多,条理也要求必须清楚,才能正确解决此题。【考点突破】【考点指要】不等式一直是高考的热点,试题大致有三类,一是考查不等式的性质,常与函数结合起来考查,有时与充要条件知识结合考查,多采用选择题形式;二是解不等式,有采用选择题或填空题的基本题,也有解答题,在解答题中,含有字母参数的不等式较多,也较难,需要对字母参数进行讨论;三是与应用题结合考查,也是高考的热点。高考所占比重约20分左右。【典型例题分析】例4....