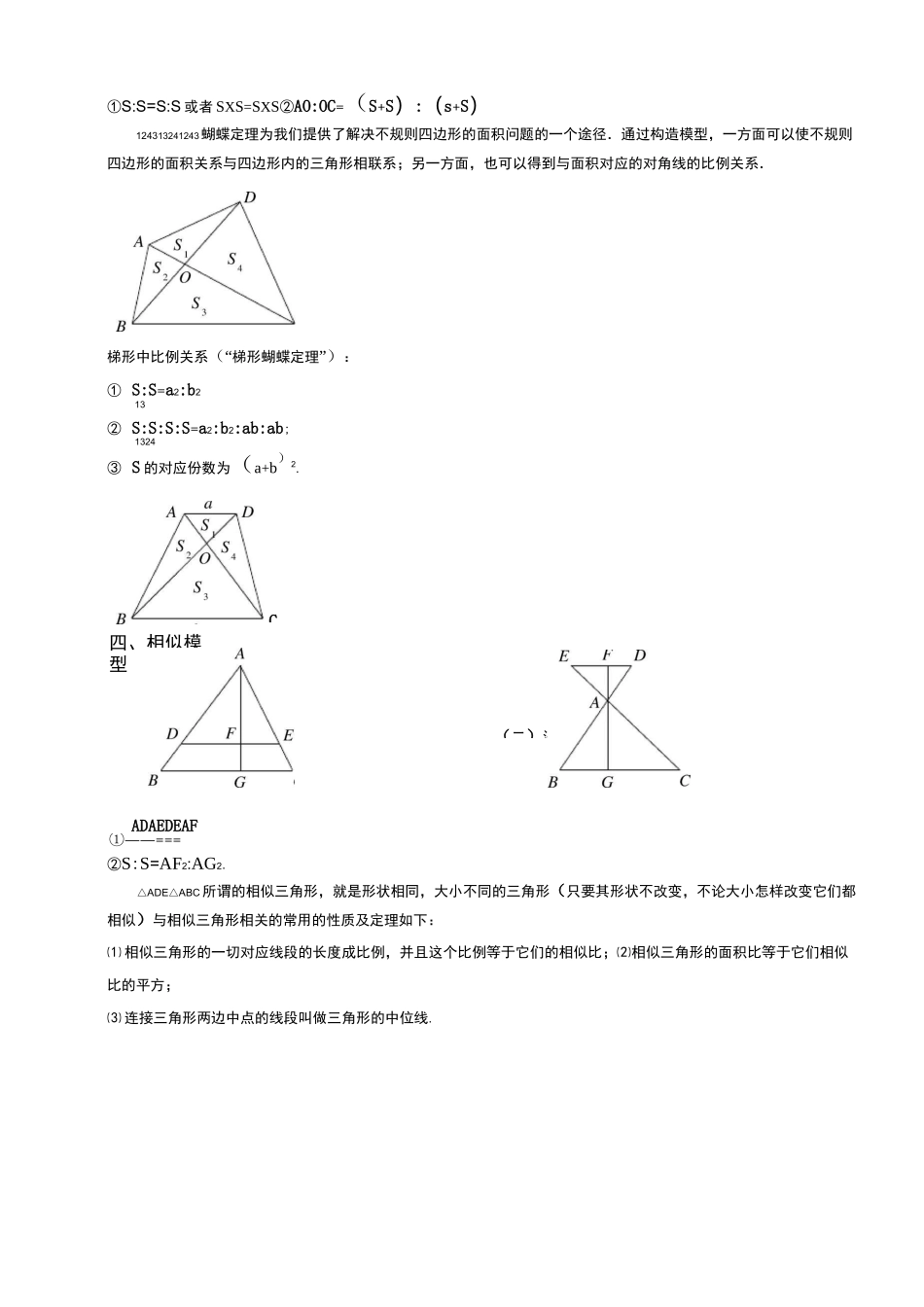
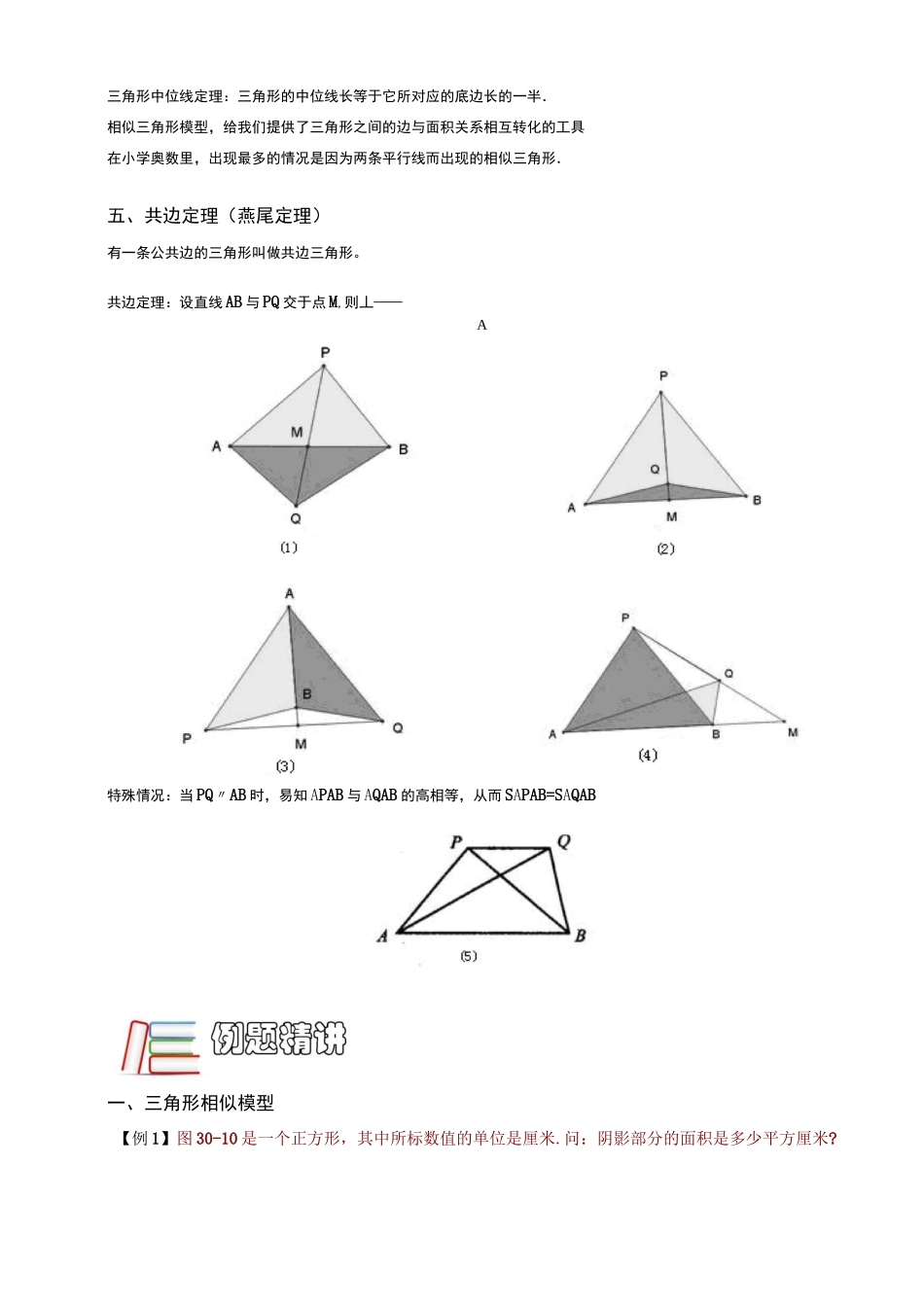
①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;③夹在一组平行线之间的等积变形,如右图.CD;反之,如果S=S,则可知直线AB平行于CD.△ACD△BCD④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、共角定理(鸟头定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比S:S=(ABXAC):(ADXAE)△ABC△ADE三、蝴蝶定理任意四边形中的比例关系“(蝴蝶定理”)一、等积模型四、相似模型(二)沙漏模①S:S=S:S或者SXS=SXS②AO:OC=(S+S):(s+S)124313241243蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系“(梯形蝴蝶定理”):①S:S=a2:b213②S:S:S:S=a2:b2:ab:ab;1324③S的对应份数为(a+b)2.②S:S=AF2:AG2.△ADE△ABC所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似)与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.CADAEDEAF——①===三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾定理)有一条公共边的三角形叫做共边三角形。共边定理:设直线AB与PQ交于点M,则丄——A特殊情况:当PQ〃AB时,易知APAB与AQAB的高相等,从而SAPAB=SAQAB一、三角形相似模型【例1】图30-10是一个正方形,其中所标数值的单位是厘米.问:阴影部分的面积是多少平方厘米?【例2】已知三角形ABC的面积为a,AF:FC=2:1,E是BD的中点,且EF〃BC,交CD于G,求【巩固】如图,四边形ABCD和EFGH都是平行四边形,四边形ABCD的面积是16,BG:GC=3:1,则四边形EFGH的面积=.阴影部分的面积.【巩固】图中ABCD是边长为12cm的正方形,从G到正方形顶点C、D连成一个三角形,已知这个三角形在AB上截得的EF长度为4cm,那么三角形GDC的面积是多少?【例3】如图,O是矩形一条对角线的中点,图中已经标出两个三角形的面积为3和4,那么阴影部分的一块直角三角形的面积是多少?【巩固】ABCD是平行四边形,面积为72平方厘米,E、F分别为AB、BC的中点,则图中阴影部分的面积为平方厘米.AD二、蝴蝶模型【例4】如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15四边形EFGO的面积为CB【巩固】如图5所示,矩形ABCD的面积是24平方厘米,、三角形ADM与三角形BCN的面积之和是7.8平方厘米,则四边形PMON的面积是平方厘米。【例5】如图,AABC是等腰直角三角形,DEFG是正方形,线段AB与CD相交于K点.已知正方形DEFG的面积48,AK:KB=1:3,则ABKD的面积是多少?【巩固】如图所示,ABCD是梯形,AADE面积是1.8,AABF的面积是9,ABCF的面积是27.那么阴影AAEC面积是多少?【例6】如图,在一个边长为6的正方形中,放入一个边长为2的正方形,保持与原正方形的边平行,现在分别连接大正方形的一个顶点与小正方形的两个顶点,形成了图中的阴影图形,那么阴影部分的面积为.【巩固】下图中,四边形ABCD都是边长为1的正方形,E、F、G、H分别是AB,BC,CD,DA的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m,那么,(m+n)的值等n于.三、共角定理(燕尾定理)【例7】如图所示,在四边形ABCD中,AB=3BE,AD=3AF,四边形AEOF的面积是12,那么平行四边形BODC的面积为.CEHDBFCB分别是例8】【巩固】正六边形A,A,A,A,A,A的面积是2009平方...