2015高中数学2.1.2指数函数及其性质课件4新人教A版必修1VIP免费

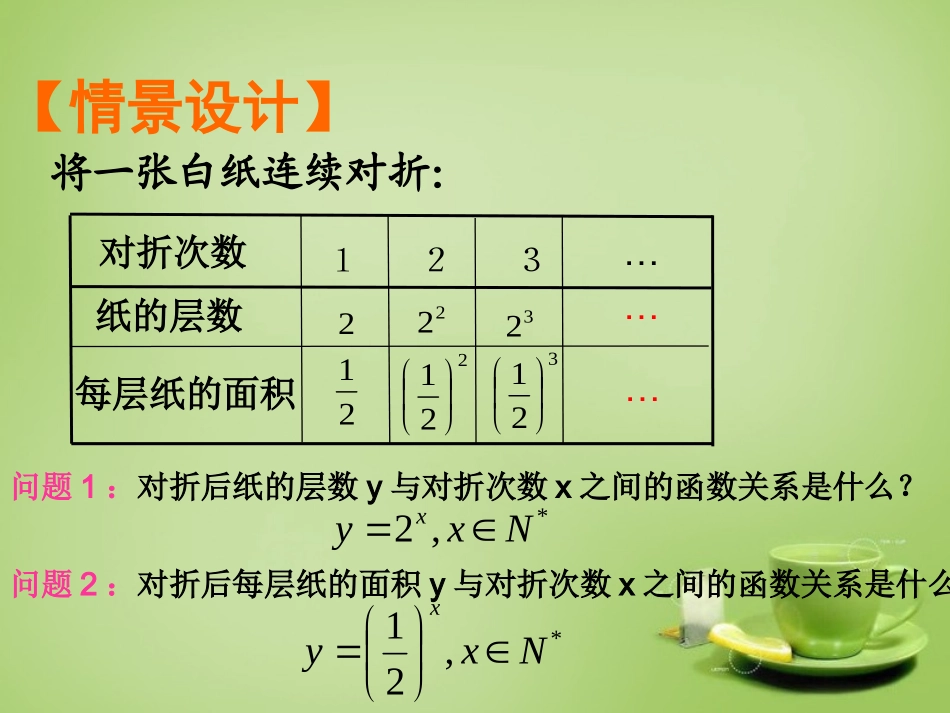
高一年级数学必修一（人教A版）【学习目标】1、理解指数函数的概念,能画出具体指数函数的图象；2、掌握指数函数的图象及性质,能应用所学知识解决简单的数学问题；【情景设计】21321221…纸的层数１２３…每层纸的面积对折次数…22232将一张白纸连续对折：问题1：对折后纸的层数y与对折次数x之间的函数关系是什么？问题2：对折后每层纸的面积y与对折次数x之间的函数关系是什么？*,2Nxyx*,21Nxyx共同特征是：●观察下列几个函数，结合上述两个例子，总结出它们的共同特征：Rxyx,2)1(Rxyx,)31()2(Rxeyx,)3(1.都是指数幂的形式3.底数是常数2.自变量在指数位置上【思考】【基础知识构建】1、指数函数的定义一般的，形如的函数叫做指数函数，其中为自变量，函数的定义域为。)10(aaayx且xR为什么要规定底数大于0且不等于1呢？当a<0时，当a=0时，当a=1时，ax恒等于1，是常函数；ax有时会没有意义，如无意义；20ax有时会没有意义，如无意义。213下列函数哪些是指数函数？【基础知识构建】4)1(xyxy)4()2(xy4)3(14)4(xyxy)5(其中是指数函数的序号有（5）判断的依据是：解析式形式是否符合指数函数的概念研究初等函数性质的基本方法和步骤：①列表②描点③连线2、研究函数性质1、画出函数图象①定义域②值域③单调性④奇偶性【思考】【合作·探究1】2、观察预习过程中画出的xy2xy21xy3xy31四个函数的图象，试着从图象中总结出指数函数的性质，完成下表。要求：小组集中讨论，力争做到人人都发言，尽量挖掘出更多的性质，时间2分钟，【合作·探究2】3、比较下列各组值的大小35.27.17.1)1(和2.01.08.08.0)2(和35.27.17.12.01.08.08.0判断的依据是：指数函数的单调性挑战1挑战3点评人展示人展示题目3组1组2组5组（1）每组的B层同学负责展示，组内的A层学生负责给C层学生讲解。（2）展示人书写规范快速，如需总结规律，请用彩笔。（3）其他同学讨论完毕总结完善，A层注意拓展，不浪费一分钟。（4）小组长要检查落实，力争全部达标。【课堂小结】通过本节课的学习，我学到了哪些新的知识？1.指数函数的概念；2.指数函数的图象与性质；3.运用指数函数性质解决比较大小问题。【课后作业】课本第59页习题2.1A组第7、8题；B组第3、4题（C层选做）