2015年秋高中数学2.5平面向量应用举例课件新人教版必修4VIP免费

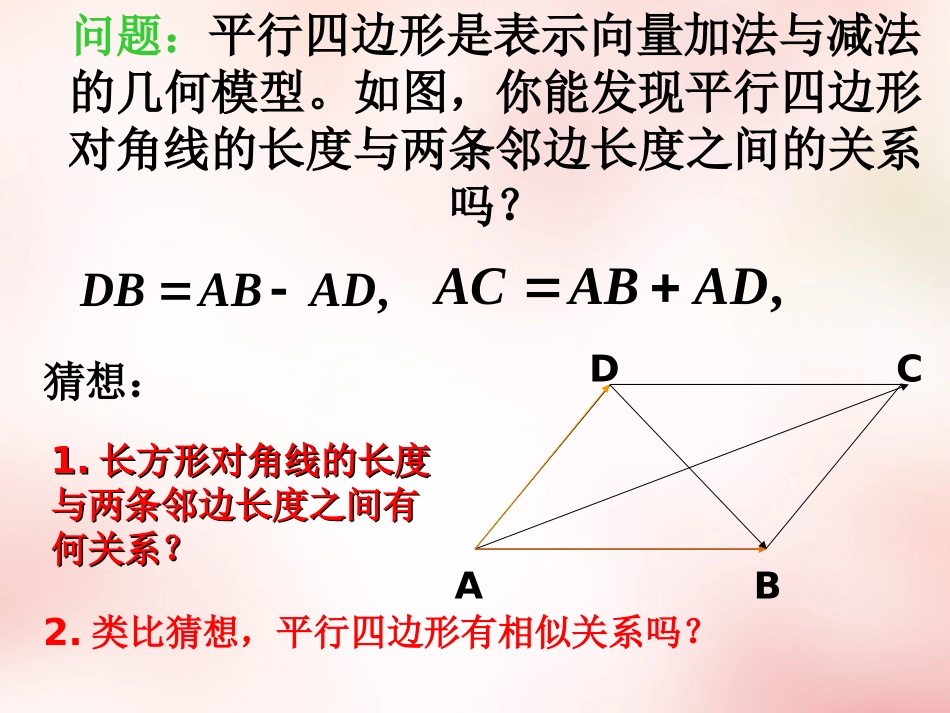
2.5平面向量应用举例2.5.1平面几何的向量方法2.5.2向量在物理中的应用举例平面几何中的向量方法由于向量的线性运算和数量积运算具有鲜明的几何背景，平面几何的许多性质，如平移、全等、相似、长度、夹角都可以由向量的线性运算及数量积表示出来，因此，利用向量方法可以解决平面几何中的一些问题。问题：平行四边形是表示向量加法与减法的几何模型。如图，你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗？,ACABAD�,DBABAD�ABCD猜想：1.1.长方形对角线的长度长方形对角线的长度与两条邻边长度之间有与两条邻边长度之间有何关系？何关系？2.类比猜想，平行四边形有相似关系吗？例1、证明平行四边形四边平方和等于两对角线平方和ABDC已知：平行四边形ABCD。求证：222222BDACDACDBCABbADaAB,解：设，则baDBbaACaDAbBC;,,分析：因为平行四边形对边平行且相等，故设其它线段对应向量用它们表示。bADaAB,)(2222222baDACDBCAB2222babaBDAC222222222222bababbaabbaa∴222222BDACDACDBCAB你能总结一下利用向量法解决平面几何问题的基本思路吗？（1）建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；（2）通过向量运算，研究几何元素之间的关系，如距离、夹角等问题；（3）把运算结果“翻译”成几何元素。用向量方法解决平面几何问题的“三步曲”：简述：形到向量向量的运算向量和数到形例2、如图，平行四边形ABCD中，点E、F分别是AD、DC边的中点，BE、BF分别与AC交于R、T两点，你能发现AR、RT、TC之间的关系吗？ABCDEFRT猜想：AR=RT=TC解：设则,,,ABaADbARr�ACab�由于与共线，故设AR�AC�(),rnabnR又因为共线，所以设EREB�与12()ERmEBmab�因为所以ARAEER�1122()rbmab1122()()nabbmab因此ABCDEFRT102()()mnmanb即,ab由于向量不共0102nmmn线，1解得：n=m=3111333,,ARACTCACRTAC�所以同理于是故AT=RT=TCABCDEFRT练习、证明直径所对的圆周角是直角ABCO如图所示，已知⊙O，AB为直径，C为⊙O上任意一点。求证∠ACB=90°分析：要证∠ACB=90°，只须证向量，即。CBAC0CBAC解：设则，由此可得：bOCaAO,baCBbaAC,babaCBAC2222baba022rr即，∠ACB=90°0CBAC思考：能否用向量坐标形式证明？ab12150010/2/dmABvkmhvkmh�例。一条河的两岸平行，河宽，一艘船从出发航行到河的正对岸处。航行的速度，水流的速度，问行驶航程最短时，所用的时间是多少？1212210/,2/.vvvvkmhvkmhvvt�����分析：如图，已知，，，求例3、02vv解：由已知条件得2212||||||96(/),vvvkmh0.5603.1(min).||96dtv所以ACB绳的拉力如何变化？绳和的过程中，渐移至竖直的位置半圆支架从水平位置逐端沿端的位置，将绳的支架上，若固定端挂在半圆形的端和的轻绳上，轻绳的两根等长，的物体系在重为例OBOACBABAOBOAG、4【思考】日常生活中,我们有时要用同样长的两根绳子挂一个物体(如图).如果绳子的最大拉力为F,物体受到的重力为G。你能否用向量的知识分析绳子受到的拉力F1的大小与两绳之间的夹角θ的关系？么？的大小怎样变化，为什逐渐增大时，11.F最小，最小值是多少？为何值时，12.F？为何值时，GF3.1（1）建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；（2）通过向量运算，研究几何元素之间的关系，如距离、夹角等问题；（3）把运算结果“翻译”成几何元素。小结：一、用向量方法解决平面几何问题的“三步曲”：二、用向量中的有关知识研究物理中的相关问题,步骤如下1.问题的转化,即把物理问题转化为数学问题.2.模型的建立,即建立以向量为主题的数学模型.3.参数的获得,即求出数学模型的有关解------理论参数值.4.问题的答案,即回到问题的初始状态,解释相关的物理现象.作业:P113，A组：1、2、3、4