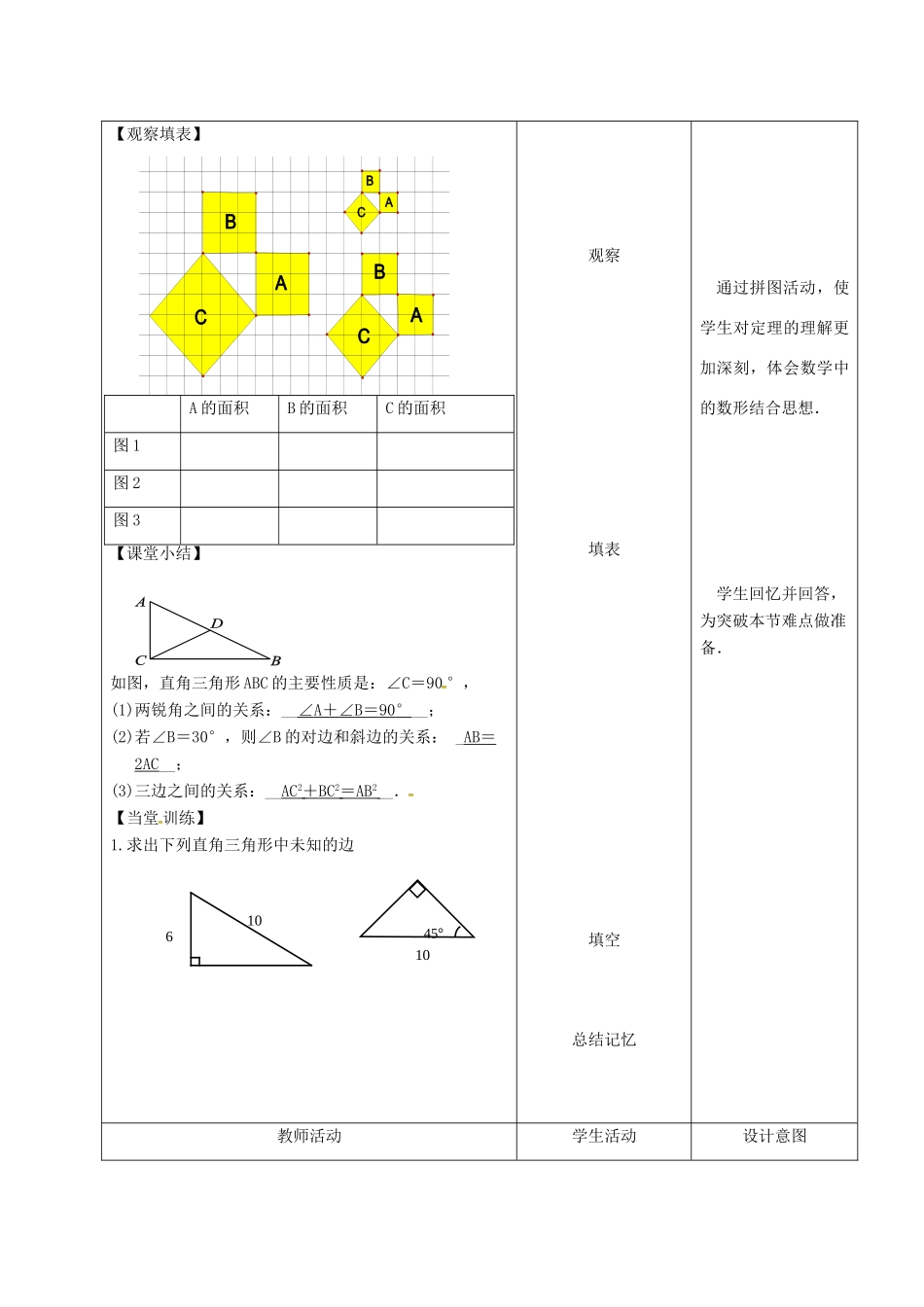
17.1勾股定理课题17.1勾股定理课时第2课时课型习题课作课时间教学内容分析本节课学习勾股定理的应用。教学目标1.通过拼图活动,使学生对定理的理解更加深刻,体会数学中的数形结合思想.2.通过习题巩固勾股定理的三边关系。重点难点掌握勾股定理的应用。教学策略选择与设计先通过拼图活动,使学生对定理的理解更加深刻,体会数学中的数形结合思想.再通过习题巩固勾股定理的三边关系。针对学生认知的差异设计了有层次的练习题,既使学生巩固知识,形成技能,又使学有余力的学生获得最佳发展.学生学习方法数形结合法,分析法,讨论法教具三角板教学过程教师活动学生活动设计意图【观察填表】A的面积B的面积C的面积图1图2图3【课堂小结】如图,直角三角形ABC的主要性质是:∠C=90°,(1)两锐角之间的关系:__∠A+∠B=90°__;(2)若∠B=30°,则∠B的对边和斜边的关系:_AB=2AC__;(3)三边之间的关系:__AC2+BC2=AB2__.【当堂训练】1.求出下列直角三角形中未知的边观察填表填空总结记忆通过拼图活动,使学生对定理的理解更加深刻,体会数学中的数形结合思想.学生回忆并回答,为突破本节难点做准备.教师活动学生活动设计意图ABCABCCBA6101045°2、填空题:在Rt△ABC,∠C=90°,⑴如果a=7,c=25,则b=。⑵如果∠A=30°,a=4,则b=。⑶如果∠A=45°,a=3,则c=。3.求下面图形中未知正方形的面积.1.求出下列各直角三角形中未知边x的长度.2.求出下列直角三角形中未知的边6.在Rt△ABC,∠C=90°⑴已知a=b=5,求c。⑵已知c=17,b=8,求a。⑶已知a=1,c=2,求b。⑷已知a:b=1:2,c=5,求a。⑸已知b=15,∠A=30°,求a,c。7.填空题⑴在Rt△ABC,∠C=90°,a=8,b=15,则c=。⑵在Rt△ABC,∠B=90°,a=3,b=4,则c=。(3)已知直角三角形的两边长分别为3cm和5cm,,则第三边长为。分析讨论读题练习1.当堂检测,及时反馈学习效果.2.针对学生认知的差异设计了有层次的练习题,既使学生巩固知识,形成技能,又使学有余力的学生获得最佳发展.1030°158分析讨论作业1、求出下列直角三角形中未知的边2、填空题⑴在Rt△ABC,∠C=90°,a=8,b=15,则c=。⑵在Rt△ABC,∠B=90°,a=3,b=4,则c=。(3)已知直角三角形的两边长分别为3cm和5cm,,则第三边长为。1030°158板书设计17.1勾股定理如图,直角三角形ABC的主要性质是:∠C=90°,(1)两锐角之间的关系:__∠A+∠B=90°__;(2)若∠B=30°,则∠B的对边和斜边的关系:_AB=2AC__;(3)三边之间的关系:__AC2+BC2=AB2__.【当堂训练】1.求出下列直角三角形中未知的边2、填空题:在Rt△ABC,∠C=90°,⑴如果a=7,c=25,则b=。⑵如果∠A=30°,a=4,则b=。⑶如果∠A=45°,a=3,则c=。教学反思6101045°