正弦和余弦()VIP免费

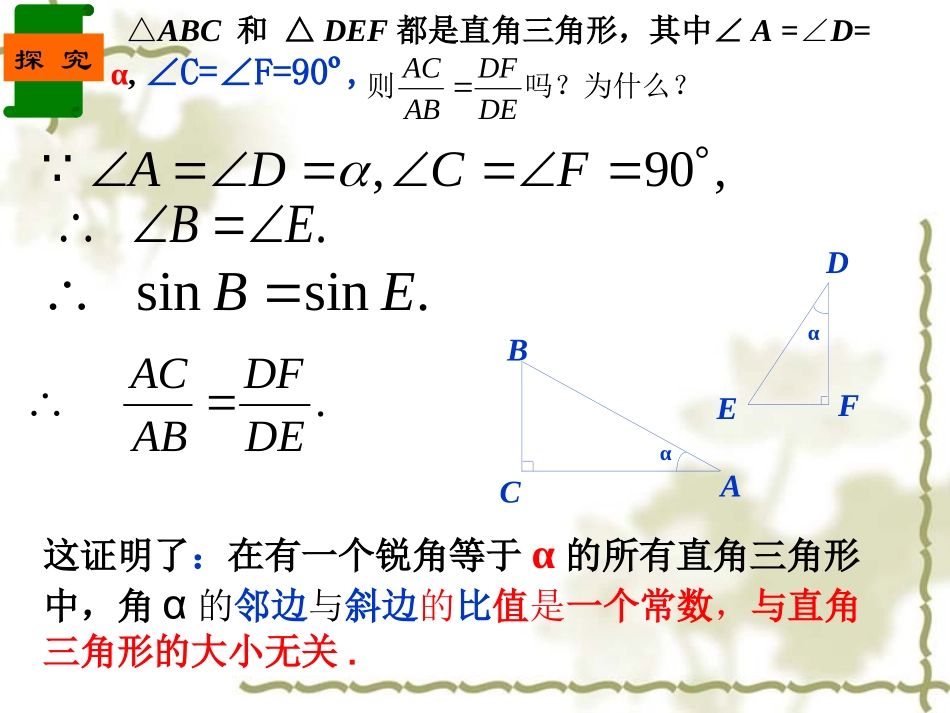
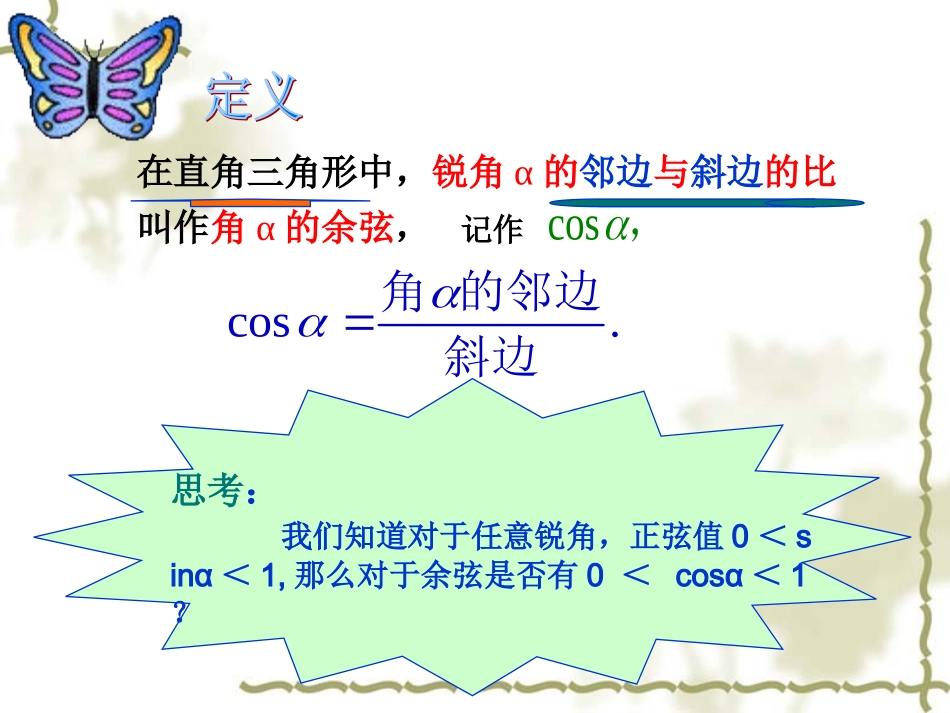
EFDαBCAα探究△ABC和△DEF都是直角三角形，其中∠A=∠D=α,∠C=∠F=90º,吗？为什么？则DEDFABAC,90,FCDA.EB.sinsinEB.DEDFABAC这证明了：在有一个锐角等于α的所有直角三角形中，角α的邻边与斜边的比值是一个常数，与直角三角形的大小无关.思考：我们知道对于任意锐角，正弦值0＜sinα＜1,那么对于余弦是否有0＜cosα＜1？在直角三角形中，锐角α的邻边与斜边的比叫作角α的余弦，记作cos，cos.角的邻边斜边1.下图中∠ACB=90°，CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.试一试：试一试：ABCD(1)sinA==AC()BC()(3)sinB==AB()CD()CDABBCAC(2)cosA==AC()AC()(4)cosB==AB()BD()ADABBCCD2．在Rt△ABC中，∠C=90º，AC=5，AB=7．求，的值．cosAcosB3．在Rt△ABC中，∠C=90º，AC=，AB=3．求，，sinA，sinBcosAcosB的值．64．对于任意锐角α，都有你能说出道理吗？0＜＜1cosBCABCA5cos,7A26cos7B6cos,3A3cos,3B3sin,3A6sin.3B∵cos,ACABAC＜AB∴0＜＜1．cos练习答案：答案：答案：根据探究的证明过程看出：对于任意锐角α，有cossin＝90-，sincos90＝．任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值.结论：互余的两角正弦值和余弦值的关系：1．求，，的值．cos30cos60cos453cos30sin9030sin60,22cos45sin9045sin45.2例题1cos60sin9060sin30,22160;2245;2330000CosCosCos结论：注：以上数值要求熟记.试一试260sin45cos2223222解：原式223223【例1】用计算器求锐角的余弦值（精确到0.0001）（1）cos30º，（2）cos50º,(3)cos15º,(4)cos55.5º主题讲解主题一、用计算器求任意角的余弦值。“cos”“55.5”“=”屏幕显示“0.566406236”按精确度要求取0.5664求锐角的余弦值（精确到0.0001）（1）cos500≈_____.(2）cos70º≈_________(3)cos15º≈_____.0.64280.34200.9659变式练习例2如何用计算器求cos75º23′？【解法1】:23′=≈0.38º∴cos75º23′≈cos75.38º≈0.25242360。【解法2】方法2.利用计算器上“D′M′S′”转化为度按键顺序（2）“cos”“75”“D′M′S′”“23”“=”显示：0.2524例3.已知cosα=0.3688，求锐角α(精确到0.01)主题二、已知一个锐角的余弦值，求这个锐角按键顺序：“2ndf”“cos”“0.3688”“=”显示：68.36练习1：求下列余弦值所对应的锐角α(精确到1′)(1)cosα=0.3279,则α≈________,(2)cosα=0.9356,则α≈_____.70º51′20º40′12sincos022AB2、在△ABC中，已知则∠C=()A30º,B45ºC60ºD105ºD小结1、用计算器求锐角的正弦和余弦时，一般的计算器是先按功能键，再按数字键。如果角度带有分，一种办法把分化为度，另一种办法利用“DMS”键。2、已知正弦或余弦值求角度时要先按“2ndf”有的计算器是按“shift”,如果要求角度化为“度”，需要按“DMS”，“=”例题讲解例4.求下列各式的值：(1)Cos45°·Sin30°－Sin45°·Cos30°(2)Sin60°－Cos30°020045cos260cos330cos.5计算：例2222213-23解：原式2200020245cos30cos21)2(;45sin60cos1）（练习：计算练习、已知等腰三角形ABC中，AB=AC=10,BC=12,求sinB,cosB的值解：作ADBC⊥于D,AB=AC,∵∴BD=DC=½BC=6.∴∴sinB=正弦和余弦的实际运用22221068ADABBD84105ADAB63cos105BDBABD解：作BH⊥AC于H(H为垂足)，则：BH=AB·Sin30°=4，H23122cmBHACS在Rt△BCH中：ABC)30°86334300CosABAHcmBCSdCHBHBCAHACCH721122723222例6.如图示，△ABC中，∠A=30°，AB=8cm，AC=6cm.3求△ABC的面积S及A到BC边的距离d.定义中应该注意的几个问题:回味无穷1、sinA、cosA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形)。2、sinA、cosA是一个比值（数值）。3、sinA、cosA的大小只与∠A的大小有关，而与直角三角形的边长无关。