正弦和余弦公开课VIP免费

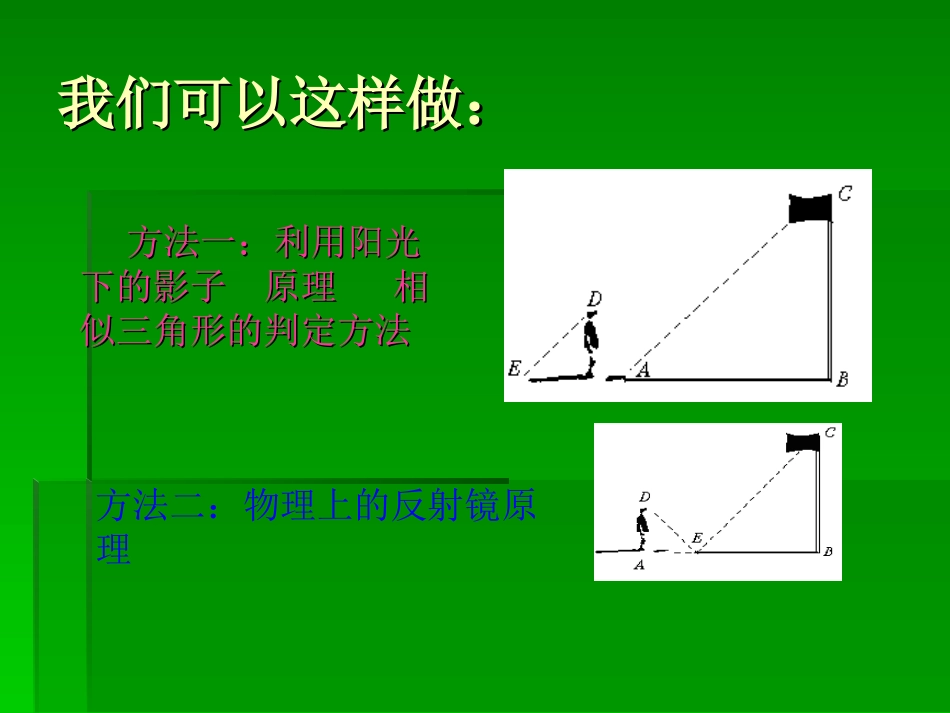
下图是学校举行升国旗仪式的情景，下图是学校举行升国旗仪式的情景，在不放倒旗杆的情况下你能想办法求在不放倒旗杆的情况下你能想办法求出旗杆的高度吗？出旗杆的高度吗？一、复习导入：一、复习导入：我们可以这样做：我们可以这样做：方法一：利用阳光方法一：利用阳光下的影子原理相下的影子原理相似三角形的判定方法似三角形的判定方法方法二：物理上的反射镜原理结论：在有一个锐角为65º的直角三角形中，65º角的对边与与斜边的比值是一个常数，它约等于0.91．的值，每位同学画一个直角三角形，其中一个锐角为65º，量出65º角的对边长度和斜边长度，计算：65角的对边斜边与同桌和邻近桌的同学交流，计算出的比值是否相等（精确到0.01）？探究结论证明已知：任意两个直角三角形△DEF和△D'E'F'，∠D=∠D'=65º，∠E=∠E'=90º求证：DEFD'E'F'∵∠E=∠E'=90º，∠D=∠D'=65º，∴△DEF∽△D'E'F'．∴EFDFEFDF证明：EFEFDFDF因此在有一个锐角为65º的所有直角三角形中，65º角的对边与斜边的比值是一个常数．于是EF·D'F'＝EF·D'F'．EFEFDFDF∴思考：若把65°角换成任意一个锐角α，则这个角的对边与斜边的比值是否也是一个常数呢？类似地可以证明：在有一个锐角等于α的所有直角三角形中，角α的对边与斜边的比值为一个常数．在直角三角形中，锐角α的对边与斜边的比叫做角α的正弦，记作:sin即:sin.角的对边斜边定义想一想：利用正弦知识你能解决我们学校旗杆的高度吗？ACB斜边c对边a1．在直角三角形ABC中，∠C=90º，BC=3，AB=5．（１）求∠A的正弦sinA；（２）求∠B的正弦sinB．CAB35例题解（１）∠A的对边BC=3，斜边AB=5．于是53sinABBCA（２）∠B的对边是AC．根据勾股定理，得222225316.ACABBC于是AC=4．因此54sinABACB1．在直角三角形ABC中，∠C=90º，BC=5，AB=13．（１）求sinA的值；（２）求sinB的值．2．小刚说：对于任意锐角α，都有你认为他说得对吗？为什么？0＜＜1sinCAB513练习CAB30°２．求的值．sin30解在直角三角形ABC中，∠C=90º，∠A=30°．于是∠A的对边1.2BCAB1sin30.2BCAB因此例题在直角三角形中，30°角所对的直角边与斜边有什么关系？说一说直角三角形中，30°角所对的直角边等于斜边的一半。6532131331313253BAC56（（20152015岳阳一模）在△岳阳一模）在△ABCABC中，中，AB=5AB=5，，BC=6BC=6，，BB为锐角且为锐角且sinB=sinB=，则，则sinC=sinC=（）（）AA、、BB、、CC、、DD、、斜边的对边角insABBCca注意：4、正弦的表示方法：60sin,sin,sin1A、ABCsin,1sin2、1、是一个整体，不能将其分开来理解。sinACB斜边c对边a邻边b2、锐角的正弦是一个比值，且0＜＜1,它没有单位,这个比值只与锐角的大小有关这个比值只与锐角的大小有关,,与三角形边长无与三角形边长无关。关。sin3、锐角的正弦是表示直角三角形中，锐角与它的对边及斜边的关系式（有变形公式）。小结正弦的定义：