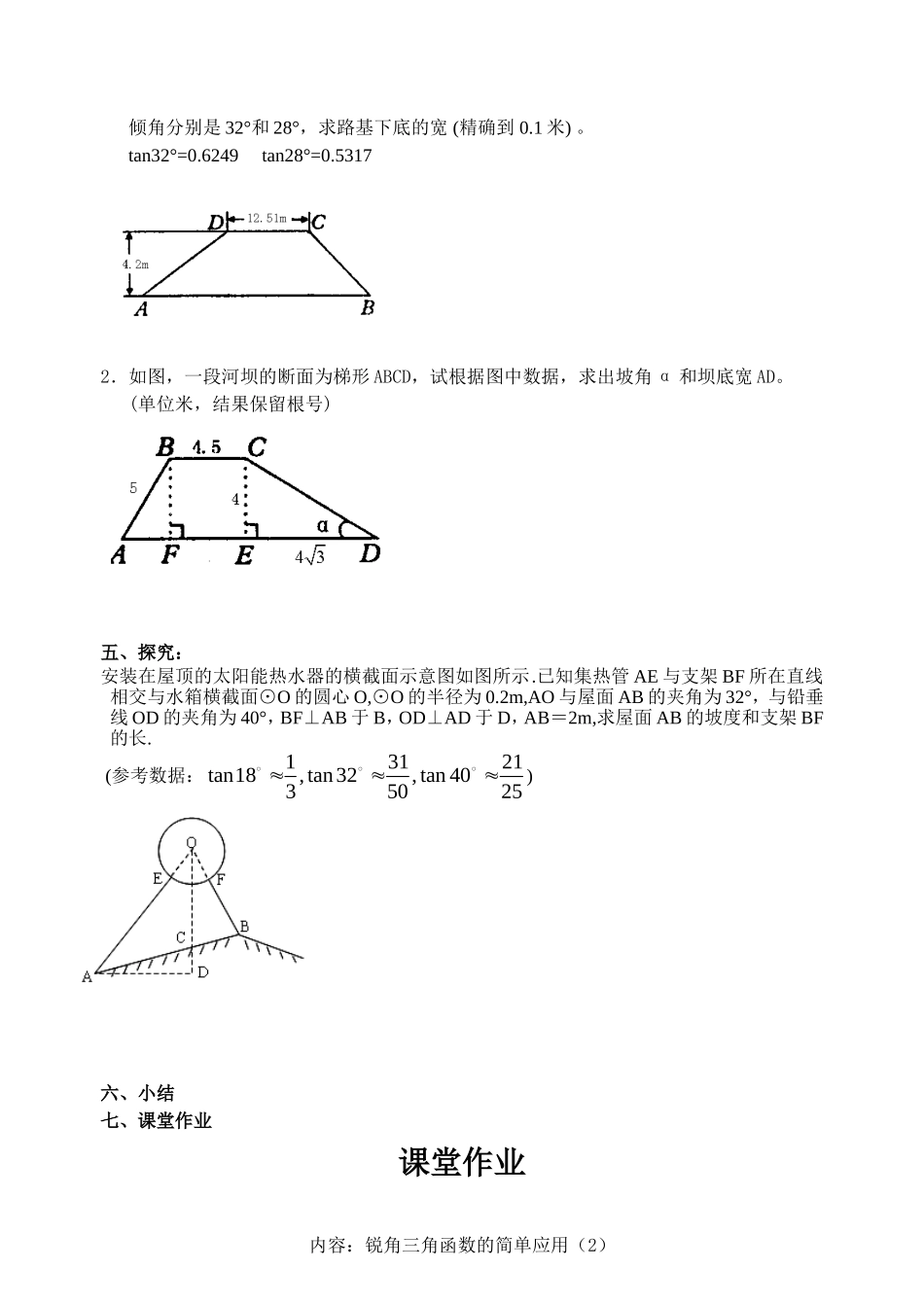
DCBA教学内容:锐角三角函数的简单应用(2)课型:新授课学生姓名:________学习目标:通过具体的一些实例,能将实际问题中的数量关系,归结为直角三角形中元素之间的关系。教学过程:一、阅读新知识:如图所示,斜坡AB和斜坡A1B1哪一个倾斜程度比较大?显然,斜坡A1Bl的倾斜程度比较大,说明∠A′>∠A。从图形可以看出,即tanAl>tanA。(注:在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度)二、坡度的概念,坡度与坡角的关系如图,这是一张水库拦水坝的横断面的设计图:_________________________________叫做坡度(或坡比),记作i,即i=________。注:坡度通常用1∶m的形式,如上图中的1:2的形式。坡面与水平面的夹角叫做坡角。从三角函数的概念可以知道:坡度与坡角的关系是i=________。显然,坡度越大,坡角_______,坡面就越_____。三、例题讲解。问题3、如图,水坝的横截面是梯形ABCD,迎水坡BC的坡角为30°背水坡AD的坡度i(即tan)为1:1,坝顶宽DC=2.5m,坝高4.5m。求:(1)背水坡AD的坡角;(2)坝底宽AB的长。拓展与延伸:如果在问题3中,为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固坝堤,要求坝顶CD加宽0.5m,水坡AD的坡度改为i为1:,已知堤坝的总长度为5km,求完成该项工程所需的土方(精确到0.1)四、练习:1.如图,一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的内容:锐角三角函数的简单应用(2)倾角分别是32°和28°,求路基下底的宽(精确到0.1米)。tan32°=0.6249tan28°=0.53172.如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角α和坝底宽AD。(单位米,结果保留根号)五、探究:安装在屋顶的太阳能热水器的横截面示意图如图所示.已知集热管AE与支架BF所在直线相交与水箱横截面⊙O的圆心O,⊙O的半径为0.2m,AO与屋面AB的夹角为32°,与铅垂线OD的夹角为40°,BF⊥AB于B,OD⊥AD于D,AB=2m,求屋面AB的坡度和支架BF的长.(参考数据:13121tan18,tan32,tan4035025)六、小结七、课堂作业课堂作业内容:锐角三角函数的简单应用(2)班级__________姓名___________学号_________得分_________1.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.75的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为()A.5mB.6mC.7mD.8m2、某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为52米,则这个破面的坡度为_________。3、如图,某人在D处测得山顶C的仰角为30o,向前走200米来到山脚A处,测得山坡AC的坡度为i=1∶0.5,求山的高度(不计测角仪的高度,31.73≈,结果保留整数).4、如图,斜坡AC的坡度(坡比)为1:3,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.5、如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角23AEF°,量得树干倾斜角38BAC°,大树被折断部分和坡面所成的角604mADCAD°,.(1)求CAE的度数;(2)求这棵大树折断前的高度?(结果精确到个位,参考数据:21.4,31.7,62.4).内容:锐角三角函数的简单应用(2)课后探究:1、京杭运河修建过程中,某村考虑到安全性,决定将运河边一河埠头的台阶进行改造.在如图的台阶横断面中,将坡面AB的坡角由45°减至30°.已知原坡面的长为6cm(BD所在地面为水平面)(1)改造后的台阶坡面会缩短多少?(2)改造后的台阶高度会降低多少?(精确到0.1m,参考数据:21.4131.73,)2、有一水库大坝的横截面是梯形ABCD,ADBCEF∥,为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,135120BADADC°,°,求水深.(精确到0.1米,21.411.73,3)3、如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.(1)求观测点B到航线l的距离;(2)求该轮船航行的速度(结果精确到0.1km/h).(参考数据:31.73≈,sin760.97°≈,cos760.24°≈,tan764.01°≈)内容:锐角三角函数的简单应用(2)