21.3二次根式的加减法1VIP免费

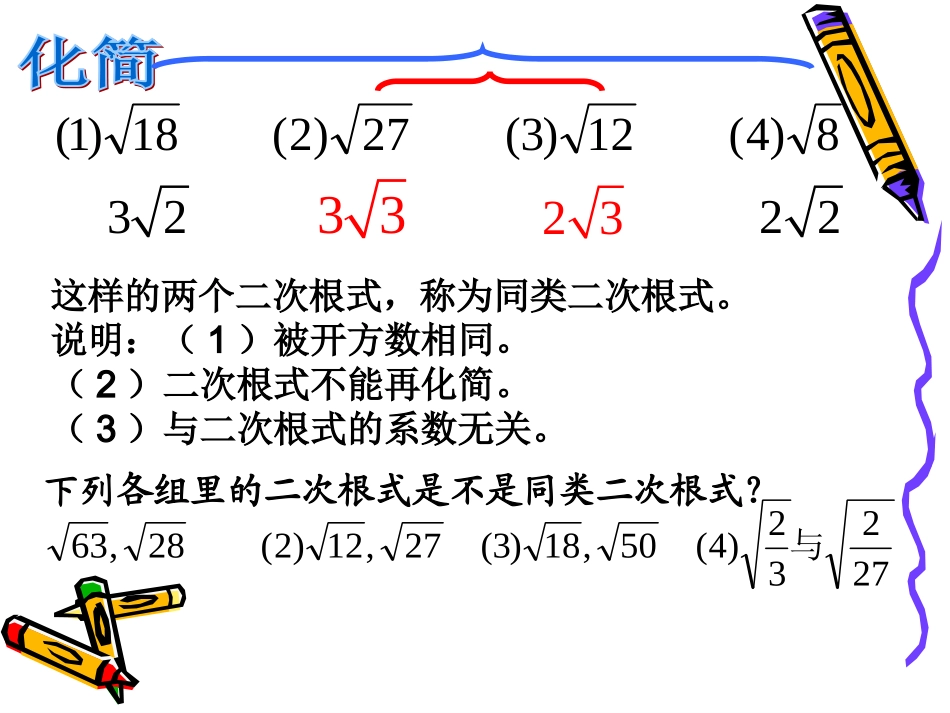
1.当x_______时，有意义．x2.____423)2(___;3233)1(:.4_____;423)2(____;23)1(:.3_____;24____;31:.2aaayyyxx猜想计算化简8)4(12)3(27)2(18)1(这样的两个二次根式，称为同类二次根式。说明：（1）被开方数相同。（2）二次根式不能再化简。（3）与二次根式的系数无关。下列各组里的二次根式是不是同类二次根式？27232)4(50,18)3(27,12)2(28,63与323323223326292____;4235273______14353___;2435373___合并同类二次根式1.化为最简二次根式2.系数相加减3.二次根式不变√√××初步应用巩固知识练习1判断下列计算是否正确？为什么？8383-=-；（1）916916=；（3）4949+=+；（2）75343-=．（4）818223223252+=+=+=（）合作探究形成知识化为最简二次根式用分配律合并整式加减二次根式性质分配律整式加减法则合作探究形成知识步骤：“一化简、二判断、三合并”；依据：二次根式的性质、分配律和整式加减法则；基本思想：把二次根式加减问题转化为整式加减问题．请总结二次根式加减的步骤、依据和基本思想．初步应用巩固知识例1计算：4199+aa；（1）8045-．（2）初步应用巩固知识例2计算（并说出运算步骤和每一步的算理）：121263483-+；（1）122035++-（）（）（2）．答案：（1）；（2）；（3）；（4）．3510233-13624-6233-初步应用巩固知识练习2计算：80205-+；（1）1240568+.--（）（）；（3）189827+-（）；（2）11323100084832-+.-（4）．综合应用深化提高练习3化简：．23549+++xxxx223=+++xxxxxx解：原式2223=++xxxx（）．1432353247275734324abab计算计算：;2218)1(;123)2(2131250)4(621562)5(21312352)6(113;182课堂练习课堂练习2763二次根式加减运算的步骤:(1)把各个二次根式化成最简二次根式(2)把各个同类二次根式合并.如何合并同类二次根式与合并同类项类似,把同类二次根式的系数相加减,做为结果的系数,根号及根号内部都不变