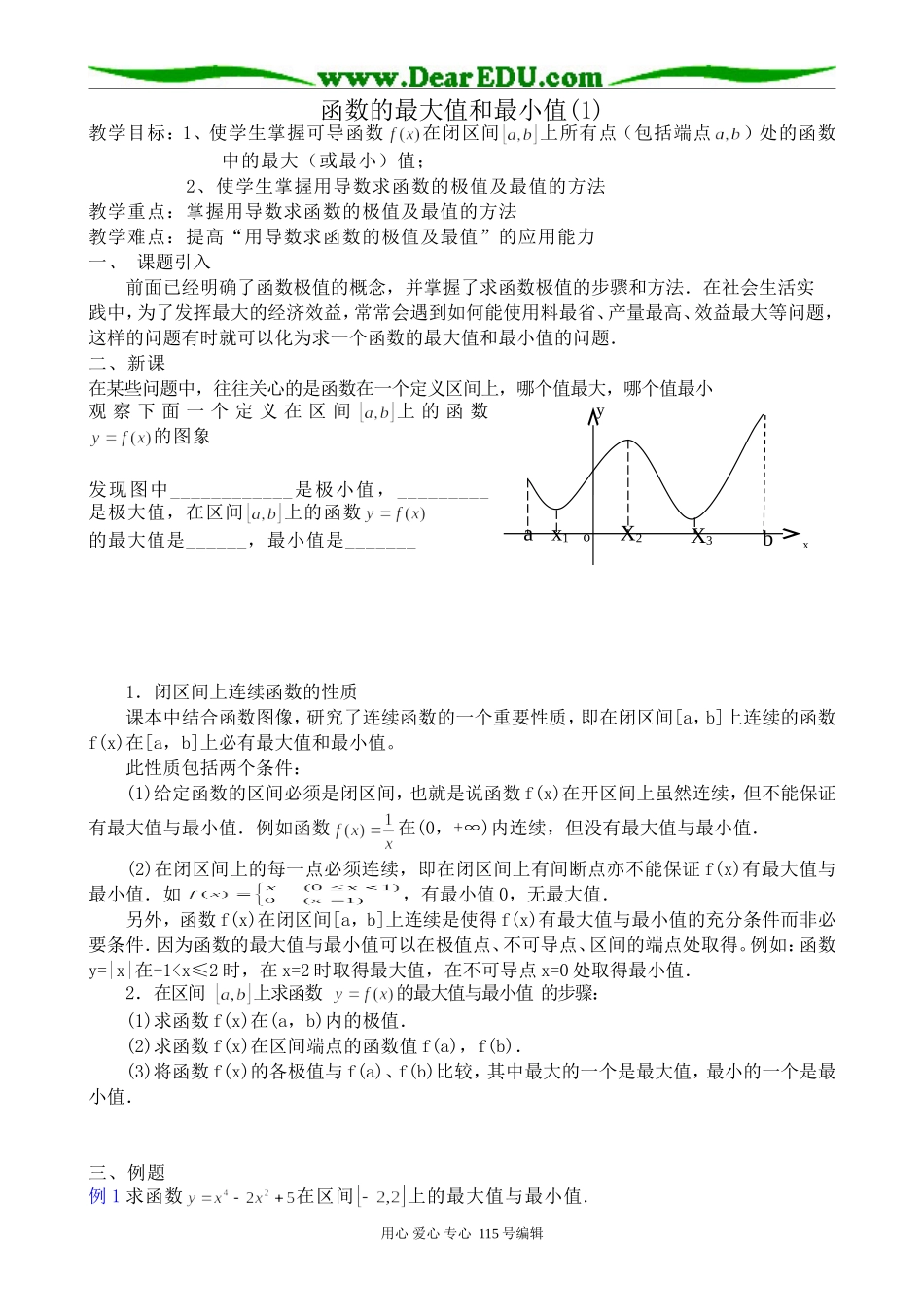
xX2oaX3bx1y函数的最大值和最小值(1)教学目标:1、使学生掌握可导函数在闭区间上所有点(包括端点)处的函数中的最大(或最小)值;2、使学生掌握用导数求函数的极值及最值的方法教学重点:掌握用导数求函数的极值及最值的方法教学难点:提高“用导数求函数的极值及最值”的应用能力一、课题引入前面已经明确了函数极值的概念,并掌握了求函数极值的步骤和方法.在社会生活实践中,为了发挥最大的经济效益,常常会遇到如何能使用料最省、产量最高、效益最大等问题,这样的问题有时就可以化为求一个函数的最大值和最小值的问题.二、新课在某些问题中,往往关心的是函数在一个定义区间上,哪个值最大,哪个值最小观察下面一个定义在区间上的函数的图象发现图中____________是极小值,_________是极大值,在区间上的函数的最大值是______,最小值是_______1.闭区间上连续函数的性质课本中结合函数图像,研究了连续函数的一个重要性质,即在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值和最小值。此性质包括两个条件:(1)给定函数的区间必须是闭区间,也就是说函数f(x)在开区间上虽然连续,但不能保证有最大值与最小值.例如函数在(0,+∞)内连续,但没有最大值与最小值.(2)在闭区间上的每一点必须连续,即在闭区间上有间断点亦不能保证f(x)有最大值与最小值.如,有最小值0,无最大值.另外,函数f(x)在闭区间[a,b]上连续是使得f(x)有最大值与最小值的充分条件而非必要条件.因为函数的最大值与最小值可以在极值点、不可导点、区间的端点处取得。例如:函数y=|x|在-10,考虑其单调性,另解:令一3x≤x10,∴,由解得01,与已知条件矛盾.若x=-1时,f(x)有最小值,则得.此时,故当时,f(x)的最小值为。综上所述,,b=1.点拨列出表格,由表格观察分析,进行分类讨论,是解决本题的关键,最后的检验不可少,因为满足条件的a、b可能是不存在的.四、小结:1、闭区间上的连续函数一定有最值;开区间内的可导函数不一定有最值,若有唯一的极值,则此极值必是函数的最值。2、函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个。3、,函数f(x)在闭区间[a,b]上连续是使得f(x)有最大值与最小值的充分条件而非必要条件.因为函数的最大值与最小值可以在极值点、不可导点、区间的端点处取得。例如:函数y=|x|在-1