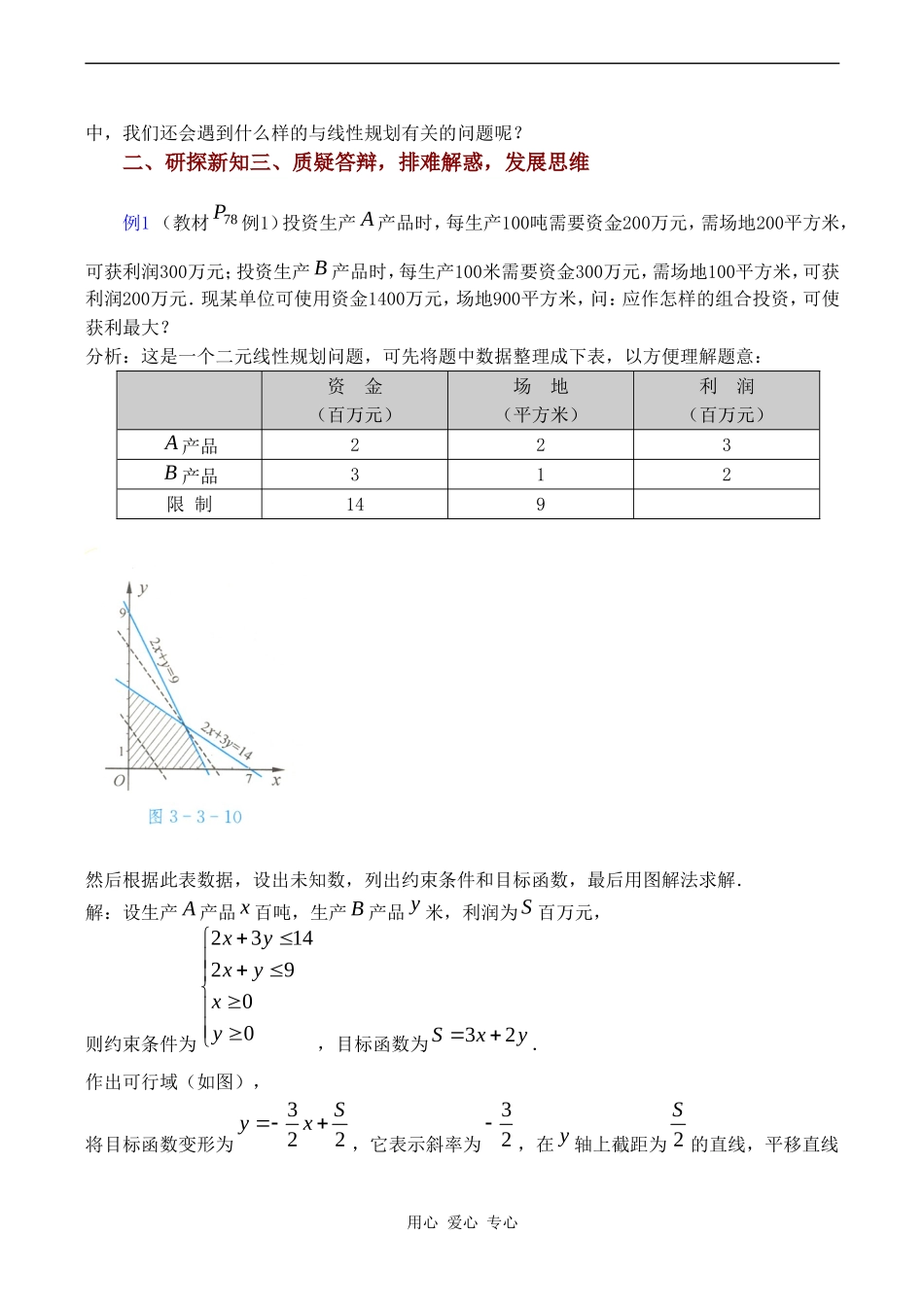
第9课时:§3.3.3简单的线性规划问题(3)【三维目标】:一、知识与技能1.能从实际情境中抽象出一些简单的二元线性规划问题,并能给出解答;2.培养学生的数学应用意识和解决问题的能力.3.培养学生观察、联想以及作图的能力,渗透化归、数形结合的数学思想,提高学生“建模”和解决实际问题的能力.二、过程与方法通过讲解实例,让学生感受线性规划中的建模问题,培养学生的应用数学的能力。三、情感、态度与价值观结合教学内容,培养学生学习数学的兴趣和“用数学”的意识,激励学生勇于创新.【教学重点与难点】:重点:将实际问题转化为线性规划问题求解(建立线性规划模型)难点:如何把实际问题转化为简单的线性规划问题,并准确给出解答.解决重点、难点的关键是根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求得最优解.为突出重点,突破难点,本节教学应指导学生紧紧抓住化归、数形结合的数学思想方法将实际问题数学化、代数问题几何化.【学法与教学用具】:1.学法:2.教学方法:为了激发学生学习的主体意识,面向全体学生,使学生在获取知识的同时,各方面的能力得到进一步的培养.根据本节课的内容特点,本节课采用启发引导、讲练结合的教学方法,着重于培养学生分析、解决实际问题的能力以及良好的学习品质.3.教学手段:新大纲明确指出:要积极创造条件,采用现代化的教学手段进行教学.根据本节知识本身的抽象性以及作图的复杂性,为突出重点、突破难点,增加教学容量,激发学生的学习兴趣,增强教学的条理性、形象性,本节课采用计算机辅助教学,以直观、生动地揭示二元一次不等式(组)所表示的平面区域以及图形的动态变化情况.4.教学用具:多媒体、实物投影仪.5.学生课前准备:坐标纸、三角板、铅笔和彩色水笔【授课类型】:新授课【课时安排】:1课时【教学思路】:一、创设情景,揭示课题复习:(1)线性规划及其有关概念是什么?(2)解线性规划问题的一般方法和步骤是什么?提问:前面我们用图解法解决了一些求线性目标函数最大值、最小值的问题.在现实生活用心爱心专心中,我们还会遇到什么样的与线性规划有关的问题呢?二、研探新知三、质疑答辩,排难解惑,发展思维例1(教材78P例1)投资生产A产品时,每生产100吨需要资金200万元,需场地200平方米,可获利润300万元;投资生产B产品时,每生产100米需要资金300万元,需场地100平方米,可获利润200万元.现某单位可使用资金1400万元,场地900平方米,问:应作怎样的组合投资,可使获利最大?分析:这是一个二元线性规划问题,可先将题中数据整理成下表,以方便理解题意:资金(百万元)场地(平方米)利润(百万元)A产品223B产品312限制149然后根据此表数据,设出未知数,列出约束条件和目标函数,最后用图解法求解.解:设生产A产品x百吨,生产B产品y米,利润为S百万元,则约束条件为23142900xyxyxy,目标函数为32Sxy.作出可行域(如图),将目标函数变形为322Syx,它表示斜率为32,在y轴上截距为2S的直线,平移直线用心爱心专心322Syx,当它经过直线与29xy和2314xy的交点135(,)42时,2S最大,也即S最大.此时,1353214.7542S.因此,生产A产品3.25百吨,生产B产品2.5米,利润最大为1475万元.说明:(1)解线性规划应用题的一般步骤:①设出未知数;②列出约束条件(要注意考虑数据、变量、不等式的实际含义及计量单位的统一);③建立目标函数;④求最优解.(2)对于有实际背景的线性规划问题,可行域通常是位于第一象限内的一个凸多边形区域,此时变动直线的最佳位置一般通过这个凸多边形的顶点.例2(教材79P例2)某运输公司向某地区运送物资,每天至少运送180吨.该公司有8辆载重为6吨的A型卡车与4辆载重为10吨的B型卡车,有10名驾驶员.每辆卡车每天往返的次数为A型车4次,B型车3次.每辆卡车每天往返的成本费为A型车320元,B型车为504元.试为该公司设计调配车辆的方案,使公司花费的成本最低.解:设每天调出A型车x辆,B型车y辆,公司花费成本z元,则约束条件为*10463101800804,xyxyxyxyN...